Giải bài 3.28 tr 151 SBT Hình học 11
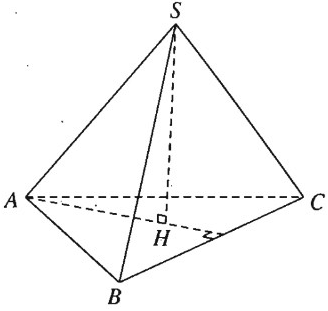
Cho hình chóp đều S.ABC. Chứng minh rằng:
a) Mỗi cạnh bên của hình chóp đó vuông góc với cạnh đối diện ;
b) Mỗi mặt phẳng chứa một cạnh bên và đường cao của hình chóp đều vuông góc với cạnh đối diện.
Hướng dẫn giải chi tiết
a) Vì S.ABC là hình chóp đều nên ∆ABC là tam giác đều và có SA = SB = SC. Do đó khi ta vẽ SH ⊥ (ABC) thì H là trọng tâm của tam giác đều ABC và ta có AH ⊥ BC. Theo định lí ba đường vuông góc ta có SA ⊥ BC.
Chứng minh tương tự ta có SB ⊥ AC và SC ⊥ AB
b) Vì BC ⊥ AH và BC ⊥ SH nên BC ⊥ (SAH)
Chứng minh tương tự ta có CA ⊥ (SBH) và AB ⊥ (SCH).
-- Mod Toán 11 HỌC247
Bài tập SGK khác
Bài tập 3.26 trang 151 SBT Hình học 11
Bài tập 3.27 trang 151 SBT Hình học 11
Bài tập 3.29 trang 151 SBT Hình học 11
Bài tập 3.30 trang 151 SBT Hình học 11
Bài tập 3.31 trang 151 SBT Hình học 11
Bài tập 3.32 trang 152 SBT Hình học 11
Bài tập 21 trang 111 SGK Hình học 11 NC
Bài tập 22 trang 111 SGK Hình học 11 NC
Bài tập 23 trang 111 SGK Hình học 11 NC
Bài tập 24 trang 111 SGK Hình học 11 NC
Bài tập 25 trang 112 SGK Hình học 11 NC
Bài tập 26 trang 112 SGK Hình học 11 NC
-


Tính góc giữa các mặt (SBC) và (ABCD) biết hình chóp SABCD có đáy là hình thoi cạnh a
bởi Nguyễn Thu Uyên
 18/04/2020
18/04/2020
Cho hình chóp SABCD có đáy là hình thoi cạnh a, góc ABC là 60 độ, SA vuông góc với đáy, SA=a căn 3. Tính góc giữa các mặt:
a) (SBC) và (ABCD);
b) (SBD) và (ABCD);
c) ( SBC) và ( SCD)
Theo dõi (0) 0 Trả lời -


 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Cho hình chóp S.ABCD có đáy ABCD là hình chử nhật AB=a BC=2a cạnh bên SA vuông góc với đáy và SA=a tính góc (sBC) và (SCD)
bởi Lê Văn Đạt
 16/04/2020
Giải dùm mình câu hình 23 vs ạ em cảm ơn
16/04/2020
Giải dùm mình câu hình 23 vs ạ em cảm ơn Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Chứng minh (SBD) vuông góc (SAC)?
bởi Kỳ Khương Nhật
 14/04/2020
14/04/2020
 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời