Nếu các em có những khó khăn về bài tập liên quan đến Góc giữa hai mặt phẳng, chứng minh hai mặt phẳng vuông góc từ bài tập SGK, Sách tham khảo, Các trang mạng cộng đồng Toán HỌC247 sẽ sớm giải đáp cho các em.
Danh sách hỏi đáp (95 câu):
-
Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD), AB là đáy lớn. I,J lần lượt là trung điểm của SA, SB. M thuộc cạnh SD.
04/12/2022 | 0 Trả lời
Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD), AB là đáy lớn. I,J lần
lượt là trung điểm của SA, SB. M thuộc cạnh SD.a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC)
b) Chứng minh rằng: IJ // (SCD).
c) Tìm giao điểm của SC và mặt phẳng (IJM).
Vẽ hình luôn giúp em . Em cảm ơn
Theo dõi (0)Gửi câu trả lời Hủy -
Cho tứ diện ABCD có AB = BC = a, AC = b, DB = DC = x, AD = y. Tìm hệ thức giữa a, b, x, y để mặt phẳng (ABC) vuông góc với Mặt phẳng (BCD).
17/11/2022 | 0 Trả lời
Cho tứ diện ABCD có AB = BC = a, AC = b, DB = DC = x, AD = y. Tìm hệ thức giữa a, b, x, y để:
a) Mặt phẳng (ABC) vuông góc với Mặt phẳng (BCD)
b) Mặt phẳng (ABC) vuông góc với Mặt phẳng (ACD)
Ai giải giúp mik với cần gấp
Theo dõi (0)Gửi câu trả lời Hủy -
Cho hình chóp S.ABCD có SA vuông góc với đáy và SA = a , đáy ABCD là hình vuông cạnh đáy a
29/04/2021 | 0 Trả lời
1 Cho hình chóp S.ABCD có SA vuông góc với đáy và SA = a , đáy ABCD là hình vuông cạnh đáy a
a) CM : (SBC) vuông góc (SAB) , (SCD) vuông góc với (SAD)
b) tính góc giữa SB và (ABCD)
SC và góc giữa (ABCD)
Theo dõi (0)Gửi câu trả lời Hủy -
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , SA vuông góc ABCD . M, N lần lượt là hình chiếu của A lên SB, SD a) Chứng minh rằng : BC vuông góc với SAB ; CD vuông góc với SAD
06/04/2021 | 2 Trả lời
Cho hình chóp sabcd có đáy là hình vuông cạnh a , sa vuông góc abcd . m,n lần lượt là hình chiếu của a lên sb,sd
a) chứng minh rằng : bc vuông góc với sab ; cd vuông góc với sad
b) chứng minh am vuông góc sbc ; an vuông góc với scd
c) chứng minh sc vuông góc với amn , và mn//bd
Theo dõi (0)Gửi câu trả lời Hủy -
 Theo dõi (0)Gửi câu trả lời Hủy
Theo dõi (0)Gửi câu trả lời Hủy -
Cho ba mặt phẳng \((\alpha)\), \((\beta )\), \((\gamma )\), mệnh dưới đây đúng hay sai: Nếu \((\alpha)\bot(\beta)\) và \((\alpha) // (\gamma)\) thì \((\beta)\bot(\gamma)\).
26/02/2021 | 1 Trả lời
Theo dõi (0)Gửi câu trả lời Hủy -
Có tồn tại một hình chóp tứ giác S.ABCD có hai mặt bên \((SAB)\) và \((SCD)\) cùng vuông góc với mặt phẳng đáy hay không ?
26/02/2021 | 1 Trả lời
Theo dõi (0)Gửi câu trả lời Hủy -
Chứng minh rằng hình chóp đều có các mặt bên là những tam giác cân bằng nhau.
26/02/2021 | 1 Trả lời
Theo dõi (0)Gửi câu trả lời Hủy -
a) Hình hộp là hình lăng trụ đứng
b) Hình hộp chữ nhật là hình lăng trụ đứng
c) Hình lăng trụ là hình hộp
d) Có hình lăng trụ không phải là hình hộp
Theo dõi (0)Gửi câu trả lời Hủy -
Theo dõi (0)Gửi câu trả lời Hủy
-
Cho hai mặt phẳng \((α)\) và \((β)\) vuông góc với nhau và cắt nhau theo giao tuyến \(d\). Chứng minh rằng nếu có một đường thẳng Δ nằm trong (α) và Δ vuông góc với d thì Δ vuông góc với (β).
25/02/2021 | 1 Trả lời
Theo dõi (0)Gửi câu trả lời Hủy -
Cho tứ diện \(ABCD\) có ba cạnh \(AB, AC, AD\) đôi một vuông góc với nhau. Chứng minh rằng các mặt phẳng \((ABC), (ACD), (ADB)\) cũng đôi một vuông góc với nhau.
25/02/2021 | 1 Trả lời
Theo dõi (0)Gửi câu trả lời Hủy -
Cho hình vuông ABCD. Dựng đoạn AS vuông góc với mặt phẳng chứa hình vuông ABCD. Hãy nêu tên các mặt phẳng lần lượt chứa các đường thẳng SB, SC, SD và vuông góc với mặt phẳng (ABCD).
26/02/2021 | 1 Trả lời
Theo dõi (0)Gửi câu trả lời Hủy -
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a SA vuông góc vs mp ( ABCD ) , SA = a √6 . a. Chứng minh rằng CD vuông góc vs mp ( SAD ).
09/02/2021 | 0 Trả lời
Câu 3. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a SA vuông góc vs mp ( ABCD ) , SA = a √6 .
a , Chứng minh rằng CD vuông góc vs mp ( SAD ) .
b , Chứng minh rằng SC vuông góc vs BD .
c . Tính góc giữa đường thẳng SC và đáy .
Theo dõi (0)Gửi câu trả lời Hủy -
Cho chóp SABC có đáy là tam giác vuông cân tại B, SA vuông góc với đáy và SA=SB=SC=a. H là trung điểm AC, BK là đường cao của tam giác SBC
07/02/2021 | 0 Trả lời
a) Chứng minh BH vuông góc (SAC),SC vuông góc (BHK)b) Tính các cạnh và diện tích của tam giác BHK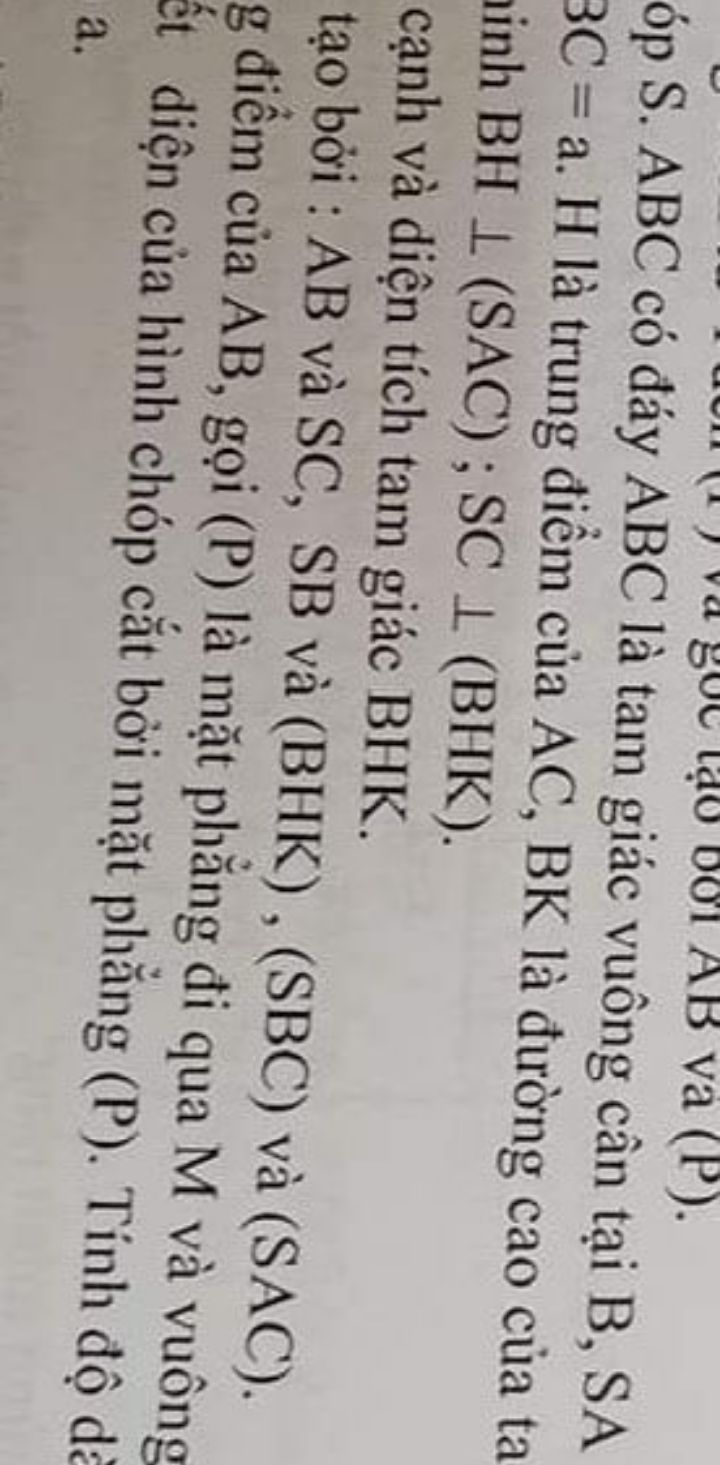 Theo dõi (0)Gửi câu trả lời Hủy
Theo dõi (0)Gửi câu trả lời Hủy -
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, cạnh bên SA=a và vuông góc với mặt phẳng đáy. Gọi M,N lần lượt là trung điểm SB và SD. Sin của góc giữa hai mặt phẳng (AMN) và (SBD) bằng?
06/02/2021 | 0 Trả lời
Cho hình chóp S.ABCD có đáy là hình vuông cạnh $#a, cạnh bên SA=a và vuông góc với mặt phẳng đáy. Gọi M,N lần lượt là trung điểm SB và SD. Sin của góc giữa hai mặt phẳng (AMN) và (SBD) bằng?
Theo dõi (0)Gửi câu trả lời Hủy -
A. Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.
B. Có duy nhất một mặt phẳng đi qua một đường thẳng cho trước và vuông góc với một mặt phẳng cho trước.
C. Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.
D. Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.
Theo dõi (0)Gửi câu trả lời Hủy -
A. Hai đường thẳng không cắt nhau, không song song thì chéo nhau.
B. Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song.
C. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì song song.
D. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song.
Theo dõi (0)Gửi câu trả lời Hủy -
Đâu là mệnh đề đúng trong các mệnh đề sau?
26/01/2021 | 1 Trả lời
A. Hai mặt phẳng vuông góc với nhau thì mọi đường thẳng nằm trong mặt phẳng này sẽ vuông góc với mặt phẳng kia.
B. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì vuông góc với nhau.
C. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
D. Hai mặt phẳng vuông góc với nhau thì mọi đường thẳng nằm trong mặt phẳng này và vuông góc với giao tuyến của hai mặt phẳng sẽ vuông góc với mặt phẳng kia.
Theo dõi (0)Gửi câu trả lời Hủy -
Chỉ ra mệnh đề đúng khi nói về đường thẳng và mặt phẳng trong các mệnh đề đã cho sau:
25/01/2021 | 1 Trả lời
A. Cho hai đường thẳng song song a và b và đường thẳng c sao cho c ⊥ a, c ⊥ b. Mọi mặt phẳng (α) chứa c thì đều vuông góc với mặt phẳng (a; b)
B. Cho a ⊥ (α) , mọi mặt phẳng (β) chứa a thì (β) ⊥ (α) .
C. Cho a ⊥ b , mọi mặt phẳng chứa b đều vuông góc với a.
D. Cho a ⊥ b , nếu a ⊂ (α) và b ⊂ (β) thì (α) ⊥ (β) .
Theo dõi (0)Gửi câu trả lời Hủy -
Cho hai đường thẳng chéo nhau a và b đồng thời a ⊥ b. Chỉ ra mệnh đề đúng trong các mệnh đề sau:
25/01/2021 | 1 Trả lời
A. mặt phẳng (Q) chứa b và đường vuông góc chung của a và b thì mp(Q) ⊥ a
B. mặt phẳng (R) chứa b và chứa đường thẳng b' ⊥ a thì mp(R) ⊥ a
C. mặt phẳng (α) chứa a, mp(β) chứa b thì (α) ⊥ (β)
D. mặt phẳng (P) chứa b thì mặt phẳng (P) ⊥ a
Theo dõi (0)Gửi câu trả lời Hủy -
Trong các mệnh đề sau đây, mệnh đề nào là đúng khi nói về đường thẳng và mặt phẳng?
26/01/2021 | 1 Trả lời
A. Hai mặt phẳng cùng song song với một mặt phẳng thứ ba thì song song với nhau.
B. Qua một đường thẳng cho trước có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước.
C. Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với hai mặt phẳng cắt nhau cho trước.
D. Hai mặt phẳng cùng vuông góc với một mặt phẳng thứ ba thì vuông góc với nhau.
Theo dõi (0)Gửi câu trả lời Hủy -
Cho hai mặt phẳng (P) và (Q) song song với nhau và một điểm M không thuộc (P) và (Q). Qua M có bao nhiêu mặt phẳng vuông góc với (P) và (Q)?
25/01/2021 | 1 Trả lời
A. 2
B. 3
C. 1
D. Vô số.
Theo dõi (0)Gửi câu trả lời Hủy -
Cho hai mặt phẳng (P) và (Q), a là một đường thẳng nằm trên (P) . Mệnh đề nào sau đây sai ?
26/01/2021 | 1 Trả lời
A. Nếu a // b với b = (P) ∩ (Q) thì a // (Q)
B. Nếu (P) ⊥ (Q) thì a // (Q)
C. Nếu a cắt (Q) thì (P) cắt (Q)
D. Nếu (P) // (Q) thì a // (Q)
Theo dõi (0)Gửi câu trả lời Hủy -
Cho hai mặt phẳng (P) và (Q) cắt nhau và một điểm M không thuộc (P) và (Q). Qua M có bao nhiêu mặt phẳng vuông góc với (P) và (Q)?
26/01/2021 | 1 Trả lời
A. 1
B. 2
C. 3
D. Vô số
Theo dõi (0)Gửi câu trả lời Hủy




