-
Câu hỏi:
Số vị trí biểu diễn các nghiệm của phương trình \(\tan \left( 2x-\frac{\pi }{3} \right)+\sqrt{3}=0\) trên đường tròn lượng giác là?
-
A.
4
-
B.
3
-
C.
2
-
D.
1
Lời giải tham khảo:
Đáp án đúng: A
Ta có \(\tan \left( 2x-\frac{\pi }{3} \right)+\sqrt{3}=0\Leftrightarrow \tan \left( 2x-\frac{\pi }{3} \right)=-\sqrt{3}\Leftrightarrow \tan \left( 2x-\frac{\pi }{3} \right)=\tan \left( -\frac{\pi }{3} \right)\)
\(\Leftrightarrow 2x-\frac{\pi }{3}=-\,\frac{\pi }{3}+k\pi \Leftrightarrow 2x=k\pi \Leftrightarrow x=\frac{k\pi }{2}\text{ }\left( k\in \mathbb{Z} \right).\)
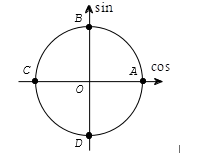
Quá dễ để nhận ra có 4 vị trí biểu diễn nghiệm của phương trình đã cho trên đường tròn lượng giác là A, B, C, D.
Hãy trả lời câu hỏi trước khi xem đáp án và lời giải -
A.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
QUẢNG CÁO
CÂU HỎI KHÁC
- Gọi S là tập nghiệm của phương trình \(2\cos x-\sqrt{3}=0\). Khẳng định nào sau đây là đúng?
- Hỏi \(x=\frac{7\pi }{3}\) là một nghiệm của phương trình nào sau đây?
- Hỏi trên đoạn \(\left[ 0;2018\pi \right]\), phương trình \(\sqrt{3}\cot x-3=0\) có bao nhiêu nghiệm?
- Trong các phương trình sau, phương trình nào tương đương với phương trình \(2{{\cos }^{2}}x=1\)?
- Phương trình nào dưới đây có tập nghiệm trùng với tập nghiệm của phương trình \({{\tan }^{2}}x=3\)?
- Trong các phương trình sau, phương trình nào tương đương với phương trình \(3{{\sin }^{2}}x={{\cos }^{2}}x\)?
- Có tất cả bao nhiêu giá trị nguyên của tham số $m$ để phương trình \(\sqrt{3}\cos x+m-1=0\) có nghiệm?
- Số nghiệm của phương trình \(\sin 2x+\sqrt{3}\cos 2x=\sqrt{3}\) trên khoảng \(\left( 0;\frac{\pi }{2} \right)\) là?
- Hàm số \(y=\frac{2\sin 2x+\cos 2x}{\sin 2x-\cos 2x+3}\) có tất cả bao nhiêu giá trị nguyên?
- Số vị trí biểu diễn các nghiệm của phương trình \(\tan \left( 2x-\frac{\pi }{3} \right)+\sqrt{3}=0\) trên đường tròn lượng giác là?
ADMICRO
ADMICRO
