-
Câu hỏi:
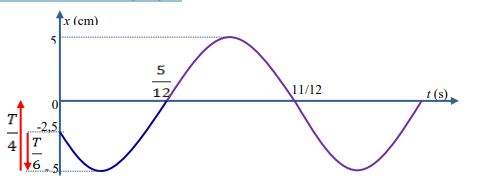
Cho dao động điều hòa có đồ thị như hình vẽ. Phương trình dao động tương ứng là:
-
A.
x = 5cos(2πt - 2π/3) cm
-
B.
x = 5cos(2πt + 2π/3) cm
-
C.
x =5cos(πt + 2π/3) cm
-
D.
x = 5cos(πt-2π/3) cm
Lời giải tham khảo:
Đáp án đúng: B
Quan sát đồ thị ta thấy: A = 5cm
\(\begin{array}{l}
\frac{5}{{12}} = \frac{T}{6} + \frac{T}{4}\\
\to T = 1s
\end{array}\)Tại thời điểm t = 0 thì x = - 2,5cm= - A/2
Và dốc xuống có nghĩa là vật đang chuyển động theo chiều âm tới vị trí biên âm nên
\(\varphi = \frac{{2\pi }}{3}\)
=> Phương trình dao động: x = 5cos(2πt + 2π/3) cm
Đáp án B
Hãy trả lời câu hỏi trước khi xem đáp án và lời giải -
A.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
CÂU HỎI KHÁC
- Biểu thức li độ của vật dao động điều hòa có dạng x = Acos(2ωt + φ), vận tốc của vật có giá trị cực đại là:
- Một chất điểm dao động điều hòa với chu kỳ 0,5π s và biên độ 2 cm. Vận tốc của chất điểm tại vị trí cân bằng có độ lớn bằng
- Biểu thức li độ của vật dao động điều hòa có dạng: x = -8cos2(2πt + π/6) cm
- Một vật đang dao động điều hòa với tần số góc 10π rad/s và biên độ √2 cm. Khi vật có vận tốc 10√10 cm/s thì gia tốc của nó có độ lớn:
- Một con lắc lò xo dao động điều hòa với chu kì T và biên độ 5 cm. Biết trong một chu kì, khoảng thời gian để vật nhỏ của con lắc có độ lớn gia tốc không vượt quá 100 cm/s2 là T/3. Lấy π2 = 10. Tần số dao động của vật là:
- Một vật nhỏ dao động điều hòa theo phương trình x = Acos4πt (t tính bằng s). Tính từ t = 0; khoảng thời gian ngắn nhất để gia tốc của vật có độ lớn bằng một nửa độ lớn gia tốc cực đại là:
- Một chất điểm dao động điều hòa trên trục Ox. Khi chất điểm đi qua vị trí cân bằng thì tốc độ của nó là 20 cm/s. Khi chất điểm có tốc độ là 10 cm/s thì gia tốc của nó có độ lớn là 40√3 cm/s2. Biên độ dao động của chất điểm
- Gia tốc của chất điểm dao động điều hoà bằng không khi nào?
- Một vật dao động điều hòa có đồ thị gia tốc như hình. Lấy π2 =10. Phương trình dao động của vật là
- Cho dao động điều hòa có đồ thị như hình vẽ. Phương trình dao động tương ứng là: