Bài tập 3.9 trang 34 SBT Toán 8 Tập 1 Kết nối tri thức - KNTT

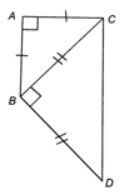
Do ∆ABC vuông cân tại đỉnh A nên $\widehat{ABC}=\widehat{ACB};$ $\widehat{A}=90°$

Xét trong ∆ABC ta có: $\widehat{ABC}+\widehat{ACB}+\widehat{A}=180°$

Nên $\widehat{ABC}=\widehat{ACB}=\frac{180°-\widehat{A}}{2}=\frac{180°-90°}{2}=45°.$

Do ∆BCD vuông cân tại đỉnh B nên $\widehat{BCD}=\widehat{BDC};$ $\widehat{CBD}=90°$

Xét trong ∆BCD ta có: $\widehat{BCD}+\widehat{BDC}+\widehat{CBD}=180°$

Nên $\widehat{BCD}=\widehat{BDC}=\frac{180°-\widehat{CBD}}{2}=\frac{180°-90°}{2}=45°.$

Ta có $\widehat{ABC}=45°=\widehat{BCD}$ nên AB // CD (hai góc so le trong bằng nhau).

Vậy ABCD là một hình thang với AB, CD là hai đáy; cạnh bên của hình thang đó là AC vuông góc với đáy AB nên hình thang đó là hình thang vuông.

-- Mod Toán 8 HỌC247