Bài 6 trang 22 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST

a)

Cứ 1 giờ người đó lại đi được \(v\) km.

Cứ 2 giờ người đó lại đi được \(2v\)km.

Vậy sau \(t\left( h \right)\) người đó sẽ đi được quãng đường \(v.t\) km.

Vậy ta có công thức tính \(s\)theo \(t\) như sau: \(s = v.t\) trong đó \(v\) là vận tốc, \(t\) là thời gian và \(s\) là quãng đường đi được.

b)

Với \(v = 4 \Rightarrow s = 4t\). Khi đó \(s\) là hàm số bậc nhất theo biến \(t\).

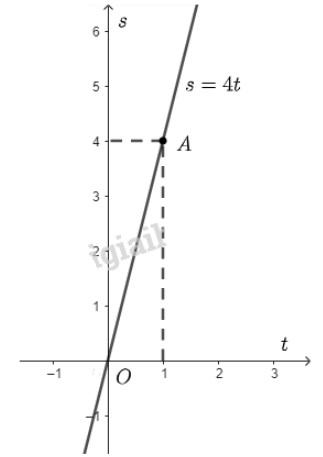
Với \(t = 1 \Rightarrow s = 4.1 = 4 \Rightarrow \) đồ thị hàm số đi qua điểm \(A\left( {1;4} \right)\).

Đồ thị hàm số \(s = 4t\) là đường thẳng đi qua hai điểm \(O\left( {0;0} \right)\) và \(A\left( {1;4} \right)\).

-- Mod Toán 8 HỌC247