Giải bài 7 trang 46 SGK Toán 6 Chân trời sáng tạo tập 1 - CTST
a) Hoàn thiện bảng sau vào vở.
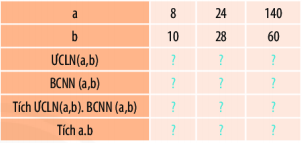
b) Nhận xét về tích ƯCLN(a, b). BCNN(a, b) và tích a. b.
Hướng dẫn giải chi tiết
Hướng dẫn giải
- Muốn tìm ƯCLN của hai hay nhiều số lớn hơn 1, ta thực hiện ba bước sau:
Bước 1: Phân tích mỗi số ra thừa số nguyên tố.
Bước 2: Chọn ra các thừa số nguyên tố chung.
Bước 3: Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất của nó.
Tích đó là ƯCLN phải tìm.
- Muốn tìm BCNN của hai hay nhiều số lớn hơn 1, ta thực hiện ba bước sau:
Bước 1: Phân tích mỗi số ra thừa số nguyên tố.
Bước 2: Chọn ra các thừa số nguyên tố chung và riêng.
Bước 3: Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ lớn nhất của nó.
Tích đó là BCNN phải tìm.
Lời giải chi tiết
a)
+) Ta có: 8 = 23, 10 = 2.5
⇒ƯCLN(8, 10) = 2
⇒BCNN(8, 10) = 23.5 = 40.
⇒ƯCLN(8, 10).BCNN(8, 10) = 2.40 = 80.
+) 24 = 23.3, 28 = 22.7
⇒ƯCLN(24, 28) = 22 = 4
⇒BCNN(24, 28) = 23.3.7 = 168.
⇒ƯCLN(24, 28).BCNN(24, 28) = 4.168 = 672
+) 140 = 22.5.7; 60 = 22.3.5
⇒ƯCLN(140, 60) = 22.5 =20
⇒BCNN(140, 60) = 22.3.5.7 = 420.
⇒ƯCLN(140, 60).BCNN(140, 60) = 20.420 = 8 400.
Ta hoàn thiện bảng sau:
|
a |
8 |
24 |
140 |
|
b |
10 |
28 |
60 |
|
ƯCLN(a, b) |
2 |
4 |
20 |
|
BCNN(a, b) |
40 |
168 |
420 |
|
ƯCLN(a, b) . BCNN(a, b) |
80 |
672 |
8400 |
|
a.b |
80 |
672 |
8400 |
b)
Dựa vào bảng vừa hoàn thành ta có nhận xét sau:
ƯCLN(a, b) . BCNN(a, b) = a . b.
-- Mod Toán 6 HỌC247
Bài tập SGK khác
Giải bài 5 trang 46 SGK Toán 6 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 46 SGK Toán 6 Chân trời sáng tạo tập 1 - CTST
Giải bài 8 trang 47 SGK Toán 6 Chân trời sáng tạo tập 1 - CTST
Giải bài 9 trang 47 SGK Toán 6 Chân trời sáng tạo tập 1 - CTST
Giải bài 1 trang 36 SBT Toán 6 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 36 SBT Toán 6 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 36 SBT Toán 6 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 36 SBT Toán 6 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 36 SBT Toán 6 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 37 SBT Toán 6 Chân trời sáng tạo tập 1 - CTST
Giải bài 7 trang 37 SBT Toán 6 Chân trời sáng tạo tập 1 - CTST
Giải bài 8 trang 37 SBT Toán 6 Chân trời sáng tạo tập 1 - CTST
Giải bài 9 trang 37 SBT Toán 6 Chân trời sáng tạo tập 1 - CTST
-


Hãy thực hiện phép tính sau: \({\frac{9}{{14}} + \frac{8}{{21}}}\)
Theo dõi (0) 1 Trả lời -


Biết hai số \({2^3}{.3^a}\) và \({2^b}{.3^5}\) có ước chung lớn nhất là \({2^2}{.3^5}\) và bội chung nhỏ nhất là \({2^3}{.3^6}\). Hãy tìm giá trị của các số tự nhiên a và b.
bởi Thùy Nguyễn
 15/02/2022
15/02/2022
Biết hai số \({2^3}{.3^a}\) và \({2^b}{.3^5}\) có ước chung lớn nhất là \({2^2}{.3^5}\) và bội chung nhỏ nhất là \({2^3}{.3^6}\). Hãy tìm giá trị của các số tự nhiên a và b.
Theo dõi (0) 1 Trả lời -


Thực hiện tìm các số tự nhiên n sao cho 6 ⁝ (n+1).
bởi thuy linh
 16/02/2022
16/02/2022
Thực hiện tìm các số tự nhiên n sao cho 6 ⁝ (n+1).
Theo dõi (0) 1 Trả lời -


Nếu ta nhân số 12 345 679 với một số a bất kì có một chữ số, rồi nhân kết quả đó với 9 thì ta được số có 9 chữ số, mỗi chữ số đều là a, chẳng hạn khi a = 3 thì
bởi hi hi
 16/02/2022
16/02/2022
12 345 679. 3 = 37 037 037;
37 037 037. 9 = 333 333 333.
Em hãy giải thích tại sao
Theo dõi (0) 1 Trả lời -
ADMICRO


Hai số có BCNN là \({2^3}{.3^4}{.5^3}\) và ƯCLN là \({3^2}.5\). Biết một trong hai số là \({2^3}{.3^2}.5\), tìm số còn lại.
bởi Bình Nguyen
 15/02/2022
15/02/2022
Hai số có BCNN là \({2^3}{.3^4}{.5^3}\) và ƯCLN là \({3^2}.5\). Biết một trong hai số là \({2^3}{.3^2}.5\), tìm số còn lại.
Theo dõi (0) 1 Trả lời





