Thực hành 2 trang 103 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST

Phương pháp giải:

Sử dụng:

‒ Định lí 1: Trong không gian, qua một điểm nằm ngoài một đường thẳng, có một và chỉ một đường thẳng song song với đường thẳng đó.

‒ Tính chất: Có duy nhất một mặt phẳng chứa hai đường thẳng song song.

Lời giải chi tiết:

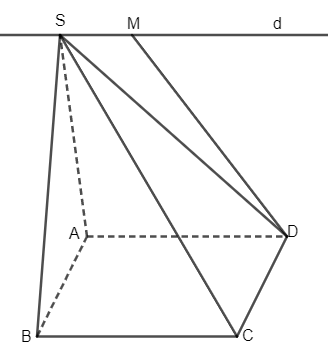
\(A{\rm{D}}M{\rm{S}}\) là hình thang có hai đáy là \(A{\rm{D}}\) và \(M{\rm{S}}\) nên \(A{\rm{D}}\parallel M{\rm{S}}\).

Theo đề bài ta lại có \(d\parallel A{\rm{D}}\).

Do đó \(d \equiv MS\) (theo định lí 1).

Lại có: \(SM \subset \left( {A{\rm{D}}M{\rm{S}}} \right) \Rightarrow d \subset \left( {A{\rm{D}}M{\rm{S}}} \right) \Rightarrow d \subset \left( {SA{\rm{D}}} \right)\).

-- Mod Toán 11 HỌC247