Hó¯Ã£ng dä¨n GiäÈi bû i täÙp ToûÀn 11 CûÀnh Diãu Chó¯óÀng 8 Bû i 5 KhoäÈng cûÀch mûÇn ToûÀn hãc lãp 11 giû¤p cûÀc em hãc sinh nä₤m vã₤ng phó¯óÀng phûÀp giäÈi bû i täÙp vû ûÇn luyãn tãt kiä¢n thãˋc.
-
HoaäÈt áûÇäÈng 1 trang 101 SGK ToûÀn 11 TäÙp 2 CûÀnh diãu - CD
Khi lä₤p thiä¢t bã cho nhû bäÀn Nam, bûÀc thÃ£È khoan tó¯Ã£ng täÀi vã trûÙ \(M\) trûˆn tó¯Ã£ng cû° áã cao so vãi nãn nhû lû \(MH = 80cm\). Quan sûÀt Hû˜nh 61, nãn nhû gãÈi nûˆn mäñt phä°ng \(\left( P \right)\), cho biä¢t áã dû i áoäÀn thä°ng \(MH\) gãÈi nûˆn khûÀi niãm gû˜ trong hû˜nh hãc liûˆn quan áä¢n áiãm \(M\) vû mäñt phä°ng \(\left( P \right)\)?

-
Luyãn täÙp 1 trang 101 SGK ToûÀn 11 TäÙp 2 CûÀnh diãu - CD
Cho hû˜nh chû°p \(S.ABC\) cû° \(SA \bot \left( {ABC} \right),AI \bot BC\left( {I \in BC} \right)\), \(AH \bot SI\left( {H \in SI} \right)\). Chãˋng minh räÝng khoäÈng cûÀch t㨠\(A\) áä¢n mäñt phä°ng \(\left( {SBC} \right)\) bäÝng \(AH\)?
-
HoäÀt áãng 2 trang 102 SGK ToûÀn 11 TäÙp 2 CûÀnh diãu - CD
Trong Hû˜nh 64, hai mûˋp cãÏa con áó¯Ã£ng gãÈi nûˆn hû˜nh äÈnh hai áó¯Ã£ng thä°ng song song \(\Delta \) vû \(\Delta '\). Xûˋt áiãm \(A\) trûˆn áó¯Ã£ng thä°ng \(\Delta \).
a) KhoäÈng cûÀch t㨠áiãm \(A\) áä¢n áó¯Ã£ng thä°ng \(\Delta '\) cû° phÃ£Ë thuãc vû o vã trûÙ cãÏa áiãm \(A\) trûˆn áó¯Ã£ng thä°ng \(\Delta \) hay khûÇng? Vû˜ sao?
b) KhoäÈng cûÀch áû° gãÈi nûˆn khûÀi niãm gû˜ trong hû˜nh hãc liûˆn quan áä¢n hai áó¯Ã£ng thä°ng song song \(\Delta \) vû \(\Delta '\)?
-
Luyãn täÙp 2 trang 102 SGK ToûÀn 11 TäÙp 2 CûÀnh diãu - CD
Ngó¯Ã£i ta dãÝng cûÀc cãt áû´n vuûÇng gû°c vãi mäñt áó¯Ã£ng, trong áû° mãi cãt áû´n gãÈi nûˆn hû˜nh äÈnh mãt áó¯Ã£ng thä°ng. KhoäÈng cûÀch giã₤a hai chûÂn cãt áû´n liûˆn tiä¢p áo áó¯Ã£Èc lû 5 m. TäÀi sao cû° thã nû°i khoäÈng cûÀch giã₤a hai cãt áû´n áû° lû 5 m?
- VIDEOYOMEDIA
-
HoäÀt áãng 3 trang 102 SGK ToûÀn 11 TäÙp 2 CûÀnh diãu - CD
Trong Hû˜nh 67, thanh gã dãc phûÙa trûˆn cûÀc cãt vû mäñt áó¯Ã£ng hû nh lang gãÈi nûˆn hû˜nh äÈnh áó¯Ã£ng thä°ng \(\Delta \) vû mäñt phä°ng \(\left( P \right)\) song song vãi nhau, chiãu cao cãÏa chiä¢c cãt cû° áãnh cãt \(A\) lû khoäÈng cûÀch t㨠áiãm \(A\) áä¢n mäñt phä°ng \(\left( P \right)\).
a) KhoäÈng cûÀch t㨠áiãm \(A\) áä¢n mäñt phä°ng \(\left( P \right)\) cû° phÃ£Ë thuãc vû o vã trûÙ cãÏa áiãm \(A\) trûˆn áó¯Ã£ng thä°ng \(\Delta \) hay khûÇng? Vû˜ sao?
b) KhoäÈng cûÀch áû° gãÈi nûˆn khûÀi niãm nû o trong hû˜nh hãc liûˆn quan áä¢n áó¯Ã£ng thä°ng \(\Delta \) vû mäñt phä°ng \(\left( P \right)\)?

-
Luyãn täÙp 3 trang 103 SGK ToûÀn 11 TäÙp 2 CûÀnh diãu - CD
Cho hû˜nh chû°p \(S.ABC\) cû° \(SA = a\), gû°c giã₤a \(SA\) vû \(mp\left( {ABC} \right)\) lû \({60^ \circ }\). Gãi \(M,N\) läÏn ló¯Ã£Èt lû trung áiãm cãÏa cäÀnh \(SA\) vû \(SB\). Chãˋng minh \(MN // \left( {ABC} \right)\) vû tûÙnh \(d\left( {MN,\left( {ABC} \right)} \right)\)?
-
HoäÀt áãng 4 trang 103 SGK ToûÀn 11 TäÙp 2 CûÀnh diãu - CD
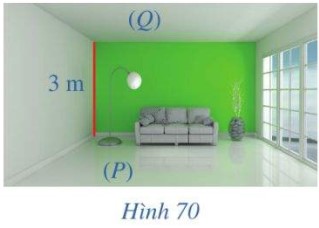
a) Trong Hû˜nh 70, sû n nhû vû träÏn nhû cãÏa cán phûýng gãÈi nûˆn hû˜nh äÈnh hai mäñt phä°ng song song \(\left( P \right),\left( Q \right)\). Chiãu cao cãÏa cán phûýng lû 3 m.
Chiãu cao áû° gãÈi nûˆn khûÀi niãm gû˜ trong hû˜nh hãc liûˆn quan áä¢n hai mäñt phä°ng song song \(\left( P \right),\left( Q \right)\)?
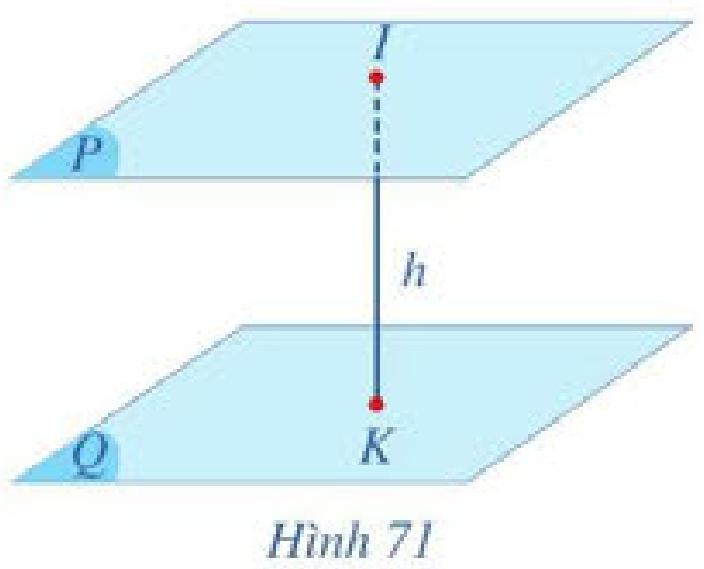
b) Cho hai mäñt phä°ng \(\left( P \right)\) vû \(\left( Q \right)\) song song vãi nhau. Xûˋt áiãm \(I\) tuã° û§ trong mäñt phä°ng \(\left( P \right)\), läËy \(K\) lû hû˜nh chiä¢u cãÏa \(I\) trûˆn \(\left( Q \right)\) (Hû˜nh 71). KhoäÈng cûÀch \(IK\) t㨠áiãm \(I\) áä¢n mäñt phä°ng \(\left( Q \right)\) cû° phÃ£Ë thuãc vû o vã trûÙ cãÏa áiãm \(I\) trong mäñt phä°ng \(\left( P \right)\) hay khûÇng? Vû˜ sao?
-
Luyãn täÙp 4 trang 104 SGK ToûÀn 11 TäÙp 2 CûÀnh diãu - CD
Cho hû˜nh láng trÃ£Ë \(ABC.A'B'C'\) cû° cäÀnh bûˆn bäÝng \(a\), gû°c giã₤a áó¯Ã£ng thä°ng \(AA'\) vû mäñt phä°ng \(\left( {ABC} \right)\) bäÝng \({60^ \circ }\). TûÙnh khoäÈng cûÀch giã₤a hai mäñt phä°ng \(\left( {ABC} \right)\) vû \(\left( {A'B'C'} \right)\)?
-
HoäÀt áãng 5 trang 105 SGK ToûÀn 11 TäÙp 2 CûÀnh diãu - CD
Trong Hû˜nh 73, khuûÇn cãÙa phûÙa trûˆn vû mûˋp cûÀnh cãÙa phûÙa dó¯Ã£i gãÈi nûˆn hû˜nh äÈnh hai áó¯Ã£ng thä°ng \(a\) vû \(b\) chûˋo nhau, hai bäÈn lã cãÏa cûÀnh cãÙa näÝm trûˆn áó¯Ã£ng thä°ng \(c\).
Quan sûÀt Hû˜nh 73 vû cho biä¢t áó¯Ã£ng thä°ng \(c\) cû° vã¨a cä₤t, vã¨a vuûÇng gû°c vãi cÃ¤È hai áó¯Ã£ng thä°ng \(a\) vû \(b\) hay khûÇng.

-
Luyãn täÙp 5 trang 106 SGK ToûÀn 11 TäÙp 2 CûÀnh diãu - CD
Cho hû˜nh chû°p tam giûÀc \(S.ABC\) cû° áûÀy \(ABC\) lû tam giûÀc áãu cäÀnh \(a,SA \bot \left( {ABC} \right)\). TûÙnh \(d\left( {SA,BC} \right)\).
-
Bû i 1 trang 106 SGK ToûÀn 11 TäÙp 2 CûÀnh diãu - CD
Hû˜nh 76 gãÈi nûˆn hû˜nh äÈnh hai mäñt phä°ng \(\left( P \right)\) vû \(\left( Q \right)\) song song vãi nhau. Cãt gã cao 4,2 m. KhoäÈng cûÀch giã₤a \(\left( P \right)\) vû \(\left( Q \right)\) lû bao nhiûˆu mûˋt?

-
Baäi 2 trang 106 SGK ToûÀn 11 TäÙp 2 CûÀnh diãu - CD
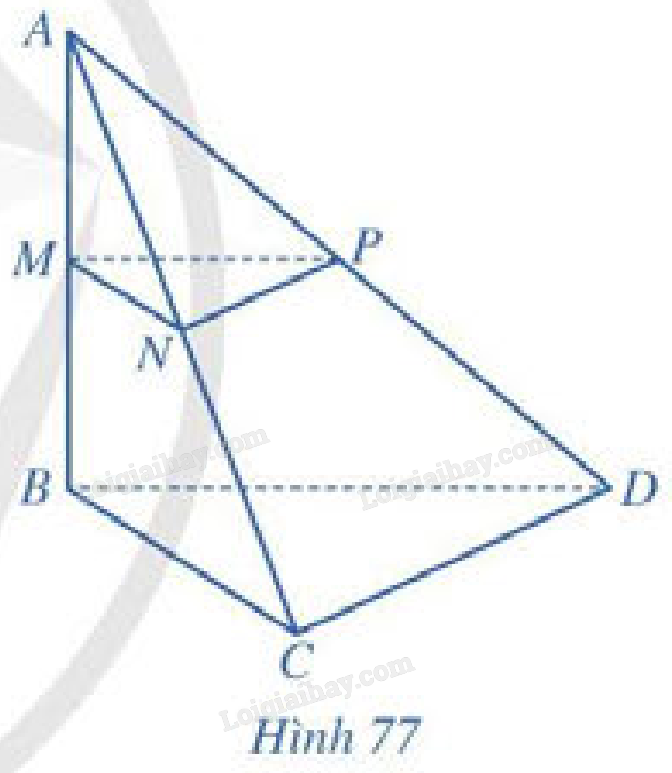
Cho hû˜nh tãˋ diãn \(ABCD\) cû° \(AB = a,BC = b,BD = c\),\(\widehat {ABC} = \widehat {ABD} = \widehat {BCD} = {90^ \circ }\). Gãi \(M,N,P\) läÏn ló¯Ã£Èt lû trung áiãm cãÏa \(AB,AC,AD\) (Hû˜nh 77).
a) TûÙnh khoäÈng cûÀch t㨠áiãm \(C\) áä¢n áó¯Ã£ng thä°ng \(AB\).
b) TûÙnh khoäÈng cûÀch t㨠áiãm \(D\) áä¢n mäñt phä°ng \(\left( {ABC} \right)\).
c) TûÙnh khoäÈng cûÀch giã₤a hai áó¯Ã£ng thä°ng \(AB\) vû \(C{\rm{D}}\).
-
Baäi 3 trang 106 SGK ToûÀn 11 TäÙp 2 CûÀnh diãu - CD
Vãi giÃ¤È thiä¢t ã Bû i täÙp 2, hûÈy:
a) Chãˋng minh räÝng \(MN\parallel BC\). TûÙnh khoäÈng cûÀch giã₤a hai áó¯Ã£ng thä°ng \(MN\) vû \(BC\).
b) Chãˋng minh räÝng \(MP\parallel \left( {BCD} \right)\). TûÙnh khoäÈng cûÀch t㨠áó¯Ã£ng thä°ng \(MP\) áä¢n mäñt phä°ng \(\left( {BCD} \right)\).
c) Chãˋng minh räÝng \(\left( {MNP} \right)\parallel \left( {BCD} \right)\). TûÙnh khoäÈng cûÀch giã₤a hai mäñt phä°ng \(\left( {MNP} \right)\) vû \(\left( {BCD} \right)\).
-
Bû i 4 trang 106 SGK ToûÀn 11 TäÙp 2 CûÀnh diãu - CD
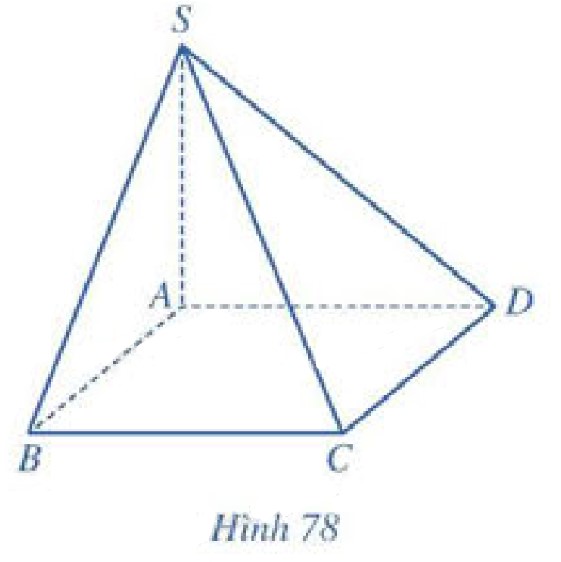
Cho hû˜nh chû°p \(S.ABCD\) cû° \(SA \bot \left( {ABCD} \right)\), áûÀy \(ABCD\) lû hû˜nh vuûÇng cäÀnh \(a\), \(SA = a\) (Hû˜nh 78).
a) TûÙnh khoäÈng cûÀch t㨠áiãm \(S\) áä¢n áó¯Ã£ng thä°ng \(C{\rm{D}}\).
b) TûÙnh khoäÈng cûÀch t㨠áiãm \(D\) áä¢n mäñt phä°ng \(\left( {SAB} \right)\).
c) TûÙnh khoäÈng cûÀch t㨠áiãm \(A\) áä¢n mäñt phä°ng \(\left( {SCD} \right)\).
-
Baäi 5 trang 106 SGK ToûÀn 11 TäÙp 2 CûÀnh diãu - CD
Vãi giÃ¤È thiä¢t ã Bû i täÙp 4, hûÈy:
a) Chãˋng minh räÝng \(BC\parallel \left( {SAD} \right)\) vû tûÙnh khoäÈng cûÀch giã₤a \(BC\) vû mäñt phä°ng \(\left( {SAD} \right)\).
b) Chãˋng minh räÝng \(BD \bot \left( {SAC} \right)\) vû tûÙnh khoäÈng cûÀch giã₤a hai áó¯Ã£ng thä°ng \(BD\) vû \(SC\).
-
Bû i tûÂäÈp 45 trang 109 SBT ToûÀn 11 TäÙp 2 Caänh diûˆäu - CD
Cho hû˜nh chã₤ nhäÙt ABCD cû° AB = 3a, AD = 4a.
a) KhoäÈng cûÀch t㨠áiãm A áä¢n áó¯Ã£ng thä°ng BC bäÝng:
A. 2,4a;
B. 3a;
C. 4a;
D. 5a.
b) KhoäÈng cûÀch t㨠áiãm A áä¢n áó¯Ã£ng thä°ng BD bäÝng:
A. 2,4a;
B. 3a;
C. 4a;
D. 5a.
c) KhoäÈng cûÀch giã₤a hai áó¯Ã£ng thä°ng AB vû CD bäÝng:
A. 2,4a;
B. 3a;
C. 4a;
D. 5a.
-
Bû i tûÂäÈp 46 trang 110 SBT ToûÀn 11 TäÙp 2 Caänh diûˆäu - CD
Hû˜nh 40 minh hoäÀ hû˜nh äÈnh mãt chiä¢c gäÙy dû i 3 m áäñt dãÝa vû o tó¯Ã£ng, gû°c nghiûˆng giã₤a chiä¢c gäÙy vû mäñt áäËt lû 65ô¯. áäÏu trûˆn cãÏa chiä¢c gäÙy áäñt vû o vã trûÙ M cãÏa tó¯Ã£ng. KhoäÈng cûÀch t㨠vã trûÙ M áä¢n mäñt áäËt (lû m trûýn kä¢t quÃ¤È áä¢n hû ng phäÏn mó¯Ã£i cãÏa mûˋt) bäÝng:
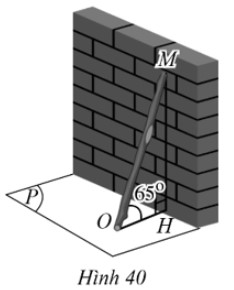
A. 2,7 m;
B. 2,8 m;
C. 2,9 m;
D. 3,0 m.
-
Bû i tûÂäÈp 47 trang 110 SBT ToûÀn 11 TäÙp 2 Caänh diûˆäu - CD
Cho hû˜nh chû°p S.ABC cû° SA ãË (ABC), AB ãË BC, SA = AB = 3a, BC = 4a. TûÙnh khoäÈng cûÀch:
a) T㨠áiãm C áä¢n mäñt phä°ng (SAB);
b) Giã₤a hai áó¯Ã£ng thä°ng SA vû BC;
c) T㨠áiãm A áä¢n mäñt phä°ng (SBC);
d) T㨠áiãm B áä¢n mäñt phä°ng (SAC);
e*) Giã₤a hai áó¯Ã£ng thä°ng AB vû SC.
-
Bû i tûÂäÈp 48 trang 110 SBT ToûÀn 11 TäÙp 2 Caänh diûˆäu - CD
Cho hû˜nh chû°p S.ABCD cû° ABCD lû hû˜nh chã₤ nhäÙt, AB = 2a, AD = 3a, tam giûÀc SAB vuûÇng cûÂn täÀi S vû näÝm trong mäñt phä°ng vuûÇng gû°c vãi (ABCD). TûÙnh khoäÈng cûÀch:
a) T㨠áiãm C áä¢n mäñt phä°ng (SAB);
b) Giã₤a hai áó¯Ã£ng thä°ng SB vû CD;
c) Giã₤a hai áó¯Ã£ng thä°ng BC vû SA;
d) T㨠áiãm S áä¢n mäñt phä°ng (ABCD).
-
Bû i tûÂäÈp 49 trang 110 SBT ToûÀn 11 TäÙp 2 Caänh diûˆäu - CD
Cho hû˜nh chû°p S.ABCD cû° ABCD lû hû˜nh vuûÇng cäÀnh a, AC cä₤t BD täÀi O, SO ãË (ABCD), SA = 2a. TûÙnh khoäÈng cûÀch:
a) T㨠áiãm A áä¢n mäñt phä°ng (SBD);
b) Giã₤a hai áó¯Ã£ng thä°ng SO vû CD;
c) T㨠áiãm O áä¢n mäñt phä°ng (SCD);
d*) Giã₤a hai áó¯Ã£ng thä°ng AB vû SD.
-
Bû i tûÂäÈp 50 trang 110 SBT ToûÀn 11 TäÙp 2 Caänh diûˆäu - CD
Cho hû˜nh hãp ABCD.AãBãCãDã cû° ABCD lû hû˜nh thoi cäÀnh a, AAã ãË (ABCD), AAã = 2a, AC = a. TûÙnh khoäÈng cûÀch:
a) T㨠áiãm A áä¢n mäñt phä°ng (BCCãBã);
b) Giã₤a hai mäñt phä°ng (ABBãAã) vû (CDDãCã);
c*) Giã₤a hai áó¯Ã£ng thä°ng BD vû AãC.


