Bài 2 trang 106 SGK Toán 11 Tập 2 Cánh diều

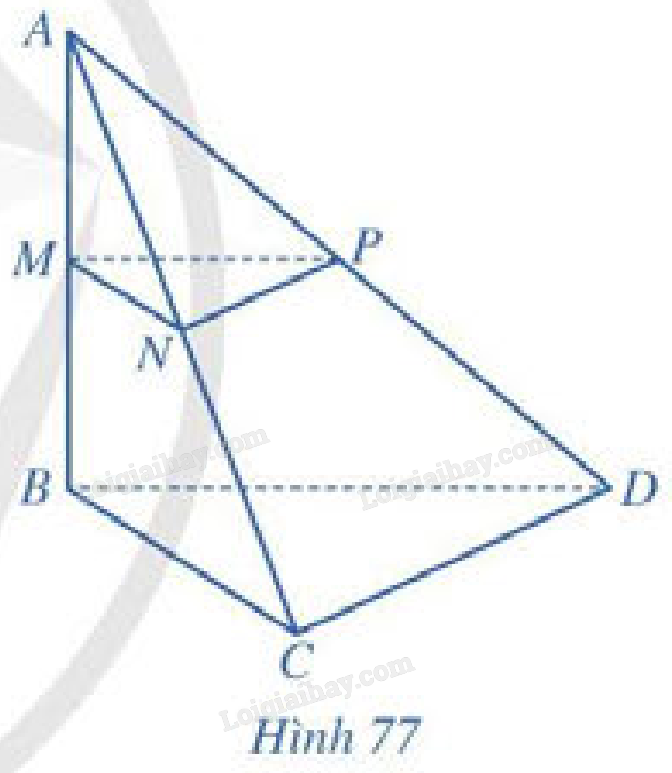
Cho hình tứ diện \(ABCD\) có \(AB = a,BC = b,BD = c\),\(\widehat {ABC} = \widehat {ABD} = \widehat {BCD} = {90^ \circ }\). Gọi \(M,N,P\) lần lượt là trung điểm của \(AB,AC,AD\) (Hình 77).

a) Tính khoảng cách từ điểm \(C\) đến đường thẳng \(AB\).

b) Tính khoảng cách từ điểm \(D\) đến mặt phẳng \(\left( {ABC} \right)\).

c) Tính khoảng cách giữa hai đường thẳng \(AB\) và \(C{\rm{D}}\).

QUẢNG CÁO

Hướng dẫn giải chi tiết Bài 2

a) Ta có: \(\widehat {ABC} = {90^ \circ } \Rightarrow AB \bot BC \Rightarrow d\left( {C,AB} \right) = BC = b\).

b) Ta có:

\(\begin{array}{l}\left. \begin{array}{l}\widehat {ABC} = {90^ \circ } \Rightarrow AB \bot BC\\\widehat {ABD} = {90^ \circ } \Rightarrow AB \bot BD\end{array} \right\} \Rightarrow AB \bot \left( {BC{\rm{D}}} \right)\\\left. \begin{array}{l} \Rightarrow AB \bot C{\rm{D}}\\\widehat {BC{\rm{D}}} = {90^ \circ } \Rightarrow BC \bot C{\rm{D}}\end{array} \right\} \Rightarrow C{\rm{D}} \bot \left( {ABC} \right)\\ \Rightarrow d\left( {D,\left( {ABC} \right)} \right) = C{\rm{D}} = \sqrt {B{{\rm{D}}^2} - B{C^2}} = \sqrt {{c^2} - {b^2}} \end{array}\)

c) Ta có: \(AB \bot BC,C{\rm{D}} \bot BC \Rightarrow d\left( {AB,C{\rm{D}}} \right) = BC = b\).

-- Mod Toán 11 HỌC247

Nếu bạn thấy hướng dẫn giải Bài 2 trang 106 SGK Toán 11 Tập 2 Cánh diều - CD HAY thì click chia sẻ