Hướng dẫn Giải bài tập Toán 11 Cánh Diều Bài 1 Đường thẳng và mặt phẳng trong không gian Toán 11 Cánh Diều giúp các em học sinh nắm vững phương pháp giải bài tập và ôn luyện tốt kiến thức.
-
Hoạt động 1 trang 85 SGK Toán 11 Cánh diều Tập 1 - CD
Sân vận động Old Trafford (Hình 2) ở thành phố Manchester, có biệt danh là “Nhà hát của những giấc mơ”, với sức chứa 75 635 người, là sân vận động lớn thứ hai ở Vương quốc Anh.
.jpg)
Quan sát Hình 2 và cho biết mặt sân vận động thường được làm phẳng hay cong?
-
Luyện tập 1 trang 86 SGK Toán 11 Cánh diều Tập 1 - CD
Nêu ví dụ trong thực tiễn minh họa hình ảnh của một phần mặt phẳng?
-
Hoạt động 2 trang 86 SGK Toán 11 Cánh diều Tập 1 - CD
Quan sát Hình 1, nếu coi mặt sân Napoléon là một phần của mặt phẳng (P) thì đỉnh của kim tự tháp có thuộc mặt phẳng (P) hay không?
.jpg)
-
Luyện tập 2 trang 87 SGK Toán 11 Cánh diều Tập 1 - CD
Vẽ hình biểu diễn của mặt phẳng (P) và đường thẳng a xuyên qua nó?
- VIDEOYOMEDIA
-
Hoạt động 3 trang 87 SGK Toán 11 Cánh diều Tập 1 - CD
Hình 9 là hình ảnh xà ngang trong môn Nhảy cao.
.jpg)
Quan sát Hình 9 và cho biết ta cần bao nhiêu điểm đỡ để giữ cố định được xà ngang đó?
-
Hoạt động 4 trang 87 SGK Toán 11 Cánh diều Tập 1 - CD
Quan sát Hình 10. Đó là hình ảnh bếp củi với kiềng ba chân. “Kiềng ba chân” là vận dụng bằng sắt, có hình vòng cung được gắn ba chân, dùng để đặt nồi lên khi nấu bếp. Bếp củi và kiềng ba chân là hình ảnh hết sức quen thuộc với gia đình ở Việt Nam. Vì sao kiềng ba chân khi đặt trên mặt đất không bị cập kênh?
.jpg)
-
Hoạt động 5 trang 89 SGK Toán 11 Cánh diều Tập 1 - CD
Hình 15 mô tả một phần của phòng học. Nếu coi bức tường chứa bảng và sàn nhà là hình ảnh của hai mặt phẳng thì giao hai mặt phẳng đó là gì?
.jpg)
-
Luyện tập 3 trang 89 SGK Toán 11 Cánh diều Tập 1 - CD
Trong Ví dụ 4 xác định giao tuyến của hai mặt phẳng (SAC) và (SBD)?
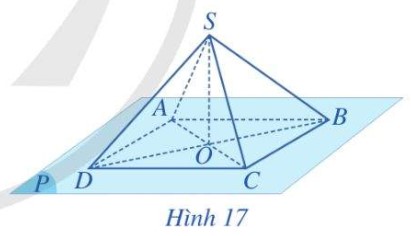
-
Hoạt động 6 trang 90 SGK Toán 11 Cánh diều Tập 1 - CD
Cho điểm A không thuộc đường thẳng d. Lấy hai điểm B và C thuộc đường thẳng d (Hình 18).
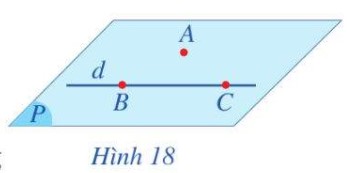
a) Mặt phẳng đi qua ba điểm A, B, C có đi qua đường thẳng d hay không?
b) Có bao nhiêu mặt phẳng đi qua điểm A và đường thẳng d?
-
Hoạt động 7 trang 90 SGK Toán 11 Cánh diều Tập 1 - CD
Cho hai đường thẳng a và b cắt nhau tại O. Lấy điểm A trên đường thẳng a (A khác O), lấy điểm B trên đường thẳng b (B khác O) (Hình 19)?
a) Mặt phẳng đi qua ba điểm A, B, O có đi qua hai đường thẳng a và b hay không?
b) Có bao nhiêu mặt phẳng đi qua hai đường thẳng a và b?
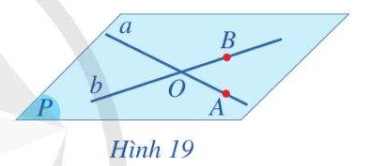
-
Luyện tập 4 trang 90 SGK Toán 11 Cánh diều Tập 1 - CD
Trong mặt phẳng (P) cho tam giác ABC. Điểm D không thuộc mặt phẳng (P). Hỏi qua hai đường thẳng AD và BC có xác định được một mặt phẳng không?
-
Hoạt động 8 trang 91 SGK Toán 11 Cánh diều Tập 1 - CD
Hình 22 là hình ảnh của một hộp quà lưu niệm có dạng hình chóp tứ giác đều \(S.ABCD\). Quan sát Hình 22 và trả lời các câu hỏi:
a) Đỉnh S có nằm trong mặt phẳng \((ABCD)\) hay không?
b) Mỗi mặt phẳng của hộp quà lưu niệm có dạng hình gì?
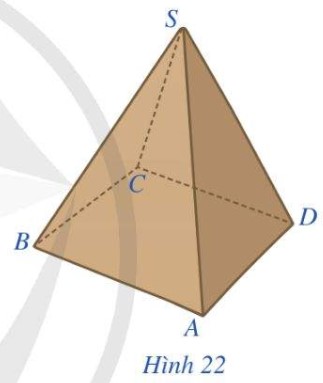
-
Luyện tập 5 trang 92 SGK Toán 11 Cánh diều Tập 1 - CD
Cho hình chóp \(S.ABCD\) có đáy là hình bình hành. Gọi M, N lần lượt là trung điểm của các cạnh SA và AD.
a) Xác định giao điểm của mặt phẳng \((CMN)\) với các đường thẳng AB, SB?
b) Xác định giao tuyến của mặt phẳng \((CMN)\) với mỗi mặt phẳng \((SAB)\) và \((SBC)\)?
-
Hoạt động 9 trang 92 SGK Toán 11 Cánh diều Tập 1 - CD
Hình 25 là hình ảnh của khối rubik tam giác (Pyraminx). Quan sát Hình 25 và trả lời các câu hỏi:
a) Khối rubik tam giác có bao nhiêu đỉnh? Các đỉnh có cùng nằm trong một mặt phẳng không?
b) Khối rubik tam giác có bao nhiêu mặt? Mỗi mặt của khối rubik tam giác là những hình gì?

-
Luyện tập 6 trang 93 SGK Toán 11 Cánh diều Tập 1 - CD
Cho tứ diện ABCD. Các điểm M, N, P lần lượt thuộc các cạnh AB, AD, BC sao cho .
a) Xác định E, F lần lượt là giao điểm của các đường thẳng AC, BD với mặt phẳng (MNP)?
b) Chứng minh rằng các đường thẳng NE, PF và CD cùng đi qua một điểm?
-
Bài 1 trang 94 SGK Toán 11 Cánh diều Tập 1 - CD
Khi trát tường, dụng cụ không thể thiếu của người thợ là thước dẹt dài (Hình 28). Công dụng của thước dẹt này là gì? Giải thích.

-
Bài 2 trang 94 SGK Toán 11 Cánh diều Tập 1 - CD
Hình 29 là hình ảnh của chặn giấy gỗ có bốn mặt phân biệt là các tam giác. Vẽ hình biểu diễn của chặn giấy bằng gỗ đó?
.jpg)
-
Bài 3 trang 94 SGK Toán 11 Cánh diều Tập 1 - CD
Cho ba đường thẳng \(a, b, c\) không cùng nằm trong một mặt phẳng và đôi một cắt nhau. Chứng minh rằng ba đường thẳng \(a, b, c\) cùng đi qua một điểm, hay còn gọi là ba đường thẳng đồng quy?
-
Bài 4 trang 94 SGK Toán 11 Cánh diều Tập 1 - CD
Cho hình chóp S.ABCD có AC cắt BD tại O và AB cắt CD tại P. Điểm M thuộc cạnh SA (M khác S, M khác A). Gọi N là giao điểm của MP và SB, I là giao điểm của MC và DN. Chứng minh rằng S, O, I thẳng hàng?
-
Bài 5 trang 94 SGK Toán 11 Cánh diều Tập 1 - CD
Cho hình chóp \(S.ABC\). Các điểm M, N lần lượt thuộc các cạnh SA, SC sao cho \(MA = 2MS,~ NS = 2NC\).
a) Xác định giao điểm của MN với mặt phẳng \((ABC)\)?
b) Xác định giao tuyến của mặt phẳng \((BMN)\) với mặt phẳng \((ABC)\)?
-
Bài 6 trang 94 SGK Toán 11 Cánh diều Tập 1 - CD
Cho hình chóp tứ giác S.ABCD có đáy không là hình thang. Gọi M là trung điểm của SA.
a) Xác định giao điểm của CD với mặt phẳng (SAB)?
b) Xác định giao tuyến của hai mặt phẳng (SAB) và (SCD)?
c) Xác định giao tuyến của hai mặt phẳng (MCD) và (SBC)?
-
Bài 7 trang 94 SGK Toán 11 Cánh diều Tập 1 - CD
Cho hình tứ diện ABCD. Gọi I là trung điểm cạnh CD. Gọi M, N lần lượt là trọng tâm các tam giác BCD, CDA.
a) Chứng minh rằng các điểm M, N thuộc mặt phẳng (ABI)?
b) Gọi G là giao điểm của AM và BN. Chứng minh rằng: ?
c) Gọi P, Q lần lượt là trọng tâm các tam giác DAB, ABC. Chứng minh rằng các đường thẳng CP, DQ cùng đi qua điểm G và ?
-
Bài tập 1 trang 94 SBT Toán 11 Tập 1 Cánh diều - CD
Cho hình chóp tứ giác \(S.ABCD\) có \(ABCD\) là hình bình hành. Điểm \(M\) thuộc cạnh \(SC\). Trong các mặt phẳng sau, điểm \(M\) nằm trên mặt phẳng nào?
A. \(\left( {ABCD} \right)\)
B. \(\left( {SAC} \right)\)
C. \(\left( {SAB} \right)\)
D. \(\left( {SAD} \right)\)
-
Bài tập 2 trang 94 SBT Toán 11 Tập 1 Cánh diều - CD
Cho hình tứ diện \(ABCD\). Giao tuyến của hai mặt phẳng \(\left( {ABC} \right)\) và \(\left( {CDA} \right)\) là đường thẳng:
A. \(AB\)
B. \(BD\)
C. \(CD\)
D. \(AC\)
-
Bài tập 3 trang 94 SBT Toán 11 Tập 1 Cánh diều - CD
Một đồ vật trang trí có bốn mặt phân biệt là các tam giác (xem hình dưới đây). Vẽ hình hiểu diễn của đồ vật đó?

-
Bài tập 4 trang 94 SBT Toán 11 Tập 1 Cánh diều - CD
Cho tứ diện \(ABCD\). Gọi \(M,{\rm{ }}N\) lần lượt là trung điểm của \(AB,{\rm{ }}CD\). Chứng minh rằng bốn điểm \(M,{\rm{ }}N,{\rm{ }}C,{\rm{ }}D\) không cùng nằm trong một mặt phẳng?
-
Bài tập 5 trang 95 SBT Toán 11 Tập 1 Cánh diều - CD
Cho hai mặt phẳng \(\left( P \right),{\rm{ }}\left( Q \right)\) cắt nhau theo giao tuyến \(d\) và hai đường thẳng \(a,{\rm{ }}b\) lần lượt nằm trong \(\left( P \right),{\rm{ }}\left( Q \right)\). Chứng minh rằng nếu hai đường thẳng \(a,{\rm{ }}b\) cắt nhau thì giao điểm của chúng thuộc đường thẳng \(d\)?
-
Bài tập 6 trang 95 SBT Toán 11 Tập 1 Cánh diều - CD
Cho tứ diện \(ABCD\). Trên các cạnh \(AC,{\rm{ }}CD\) lần lượt lấy các điểm \(E,{\rm{ }}F\) sao cho \(CE = 3EA,{\rm{ }}DF = 2FC\).
a) Xác định giao tuyến của mặt phẳng \(\left( {BEF} \right)\) với các mặt phẳng \(\left( {ABC} \right)\), \(\left( {ACD} \right)\), \(\left( {BCD} \right)\).
b) Xác định giao điểm \(K\) của đường thẳng \(AD\) với mặt phẳng \(\left( {BEF} \right)\).
c) Xác định giao tuyến của hai mặt phẳng \(\left( {BEF} \right)\) và \(\left( {ABD} \right)\).
-
Bài tập 7 trang 95 SBT Toán 11 Tập 1 Cánh diều - CD
Cho hình chóp \(S.ABCD\) có đáy là hình bình hành. Gọi \(M,{\rm{ }}N,{\rm{ }}P\) lần lượt là trung điểm của các cạnh \(SA,{\rm{ }}BC,{\rm{ }}CD\).
a) Xác định giao điểm của đường thẳng \(NP\) với mặt phẳng \(\left( {SAB} \right)\).
b) Xác định giao tuyến của mặt phẳng \(\left( {MNP} \right)\) với các mặt phẳng \(\left( {SAB} \right),{\rm{ }}\left( {SAD} \right),{\rm{ }}\left( {SBC} \right){\rm{, }}\left( {SCD} \right)\).
-
Bài tập 8 trang 95 SBT Toán 11 Tập 1 Cánh diều - CD
Cho hình chóp \(S.ABCD\) có đáy là hình bình hành. Gọi \(M,{\rm{ }}N,{\rm{ }}P\) lần lượt là trung điểm của các cạnh \(SA,{\rm{ }}SB,{\rm{ }}SC\).
a) Xác định giao điểm \(I\) của đường thẳng \(MP\) với mặt phẳng \(\left( {SBD} \right)\).
b) Xác định giao điểm \(Q\) của đường thẳng \(SD\) với mặt phẳng \(\left( {MNP} \right)\).
-
Bài tập 9 trang 95 SBT Toán 11 Tập 1 Cánh diều - CD
Cho hình chóp tứ giác \(S.ABCD\) có đáy không là hình thang. Gọi \(O\) là giao điểm của \(AC\) và \(BD\). Trên \(SO\) lấy điểm \(I\) sao cho \(SI = 2IO\).
a) Xác định các giao điểm \(M\), \(N\) lần lượt của \(SA\), \(SD\) với mặt phẳng \(\left( {IBC} \right)\).
b*) Chứng minh rằng các đường thẳng \(AD\), \(BC\) và \(MN\) đồng quy.
-
Bài tập 8 trang 95 SBT Toán 11 Tập 1 Cánh diều - CD
Cho hình chóp \(S.ABCD\) có đáy là hình bình hành. Gọi \(M,{\rm{ }}N,{\rm{ }}P\) lần lượt là trung điểm của các cạnh \(SA,{\rm{ }}SB,{\rm{ }}SC\).
a) Xác định giao điểm \(I\) của đường thẳng \(MP\) với mặt phẳng \(\left( {SBD} \right)\).
b) Xác định giao điểm \(Q\) của đường thẳng \(SD\) với mặt phẳng \(\left( {MNP} \right)\).
-
Bài tập 9 trang 95 SBT Toán 11 Tập 1 Cánh diều - CD
Cho hình chóp tứ giác \(S.ABCD\) có đáy không là hình thang. Gọi \(O\) là giao điểm của \(AC\) và \(BD\). Trên \(SO\) lấy điểm \(I\) sao cho \(SI = 2IO\).
a) Xác định các giao điểm \(M\), \(N\) lần lượt của \(SA\), \(SD\) với mặt phẳng \(\left( {IBC} \right)\).
b*) Chứng minh rằng các đường thẳng \(AD\), \(BC\) và \(MN\) đồng quy.


