Bû i Phûˋp tûÙnh léˋy thã¨a lû mãt bû i toûÀn toûÀn hãc thuãc chó¯óÀng trû˜nh mûÇn ToûÀn 11 ChûÂn trãi sûÀng täÀo, nóÀi cûÀc em áó¯Ã£Èc giãi thiãu vã khûÀi niãm vû quy tä₤c tûÙnh toûÀn léˋy thã¨a. Ngoû i ra, cûÀc em hãc sinh céˋng sä§ áó¯Ã£Èc lû m quen vãi cûÀc tûÙnh chäËt quan trãng cãÏa léˋy thã¨a. CûÀc kiä¢n thãˋc nû y sä§ giû¤p hãc sinh nä₤m vã₤ng cûÀch tûÙnh toûÀn léˋy thã¨a vû ûÀp dãËng chû¤ng vû o cûÀc bû i toûÀn thãÝc tä¢.
Tû°m tä₤t lû§ thuyä¢t
1.1. Léˋy thã¨a vãi sã méˋ nguyûˆn
- ã cäËp Trung hãc cóÀ sã, chû¤ng ta áûÈ biä¢t luã¿ thã¨a vãi sã méˋ tÃ£Ý nhiûˆn:
\[a^n = \underbrace{a\cdot a\cdots a}_{n\text{ thã¨a sã}}, \, a^0=1 (a\ne 0).\]
- Vãi n lû mãt sã nguyûˆn dó¯óÀng, a lû sã thãÝc khûÀc 0, léˋy thã¨a cãÏa a vãi sã méˋ -n xûÀc áãnh bãi:
|
\[ a ^{-n} = {1\over a^n}.\] |
Chû¤ û§:
+) \(a^0=1 \) vãi mãi \(a\in R, a\ne 0\).
+) \(0^0\) vû \(0^{-n} (n \in N)\) khûÇng cû° ngháˋa.
1.2. Cán bäÙc n
|
Cho sã nguyûˆn dó¯óÀng n (n ãË 2) vû sã thãÝc b bäËt kû˜. Nä¢u cû° sã thãÝc a sao cho \[a^n=b\] thû˜ a áó¯Ã£Èc gãi lû mãt cán bäÙc n cãÏa b. |
Chû¤ û§: ã cäËp Trung hãc cóÀ sã ta áûÈ biä¢t:
+) Nä¢u b > 0 thû˜ b cû° hai cán bäÙc hai, kûÙ hiãu lû \(\sqrt b\) (gãi lû cán bäÙc hai sã hãc cãÏa b) vû \(-\sqrt b\);
+) Sã 0 chã cû° duy nhäËt mãt cán bäÙc hai lû chûÙnh nû°;
+) Nä¢u b < 0 thû˜ b khûÇng cû° cán bäÙc hai nû o;
+) Mãi sã thãÝc b cû° duy nhäËt mãt cán bäÙc ba, kûÙ hiãu lû \(\sqrt[3] b\).
Mã rãng kä¢t quÃ¤È nû y, ta cû°:
Cho n lû sã nguyûˆn dó¯óÀng (n ãË 2), b lû sã thãÝc bäËt kû˜. Khi áû°:
ã Nä¢u n lû sã chäçn thû˜:
+ b < 0: khûÇng tãn täÀi cán bäÙc n cãÏa b.
+ b=0): cû° mãt cán bäÙc n cãÏa b lû 0.
+ b > 0): cû° hai cán bäÙc n cãÏa b áãi nhau, kûÙ hiãu giûÀ trã dó¯óÀng lû \(\sqrt[n] b\) vû giûÀ trã ûÂm lû \(-\sqrt[n] b\).
ã Nä¢u n lû sã lä£ thû˜ cû° duy nhäËt mãt cán bäÙc n cãÏa b, kûÙ hiãu \(\sqrt[n] b\).
Chû¤ û§:
+) Nä¢u n chäçn thû˜ cán thãˋc \(\sqrt[n] b\) cû° ngháˋa chã khi b > 0.
+) Nä¢u n lä£ thû˜ cán thãˋc \(\sqrt[n] b\) luûÇn cû° ngháˋa vãi mãi sã thãÝc b.
Ta cû° cûÀc tûÙnh chäËt sau áûÂy (vãi áiãu kiãn cûÀc cán thãˋc áãu cû° ngháˋa):
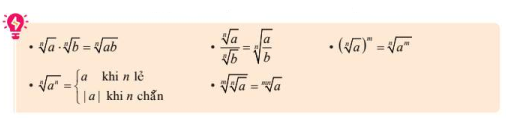
1.3. Léˋy thã¨a vãi sã méˋ hã₤u tã
|
Cho sã thãÝc a dó¯óÀng vû sã hã₤u tã \(r = \frac{m}{n}\) trong áû° m lû mãt sã nguyûˆn vû n lû sã nguyûˆn dó¯óÀng. Luã¿ thã¨a cãÏa a vãi sã méˋ r, kûÙ hiãu lû \(a^r\), xûÀc áãnh bãi \[{a^r} = {a^{\frac{m}{n}}} = \sqrt[n]{{{a^m}}}.\] |
1.4. Léˋy thã¨a vãi sã méˋ thãÝc
|
Cho a lû sã thãÝc dó¯óÀng vû \(\alpha\) lû mãt sã vûÇ tã. Xûˋt dûÈy sã hã₤u tã (\(r_n\) ) mû \(\mathop {\lim }\limits_{n \to + \infty } {r_n} = \alpha \). Luã¿ thã¨a cãÏa sã thãÝc dó¯óÀng a vãi sã méˋ \(\alpha\), kûÙ hiãu lû \(a^\alpha\). \[{a^\alpha } = \mathop {\lim }\limits_{n \to + \infty } {a^{{r_n}}}.\] |
Chû¤ û§: \({1^\alpha } =1\) vãi mãi \(\alpha \in R\).
1.5. TûÙnh chäËt cãÏa phûˋp tûÙnh léˋy thã¨a
Phûˋp tûÙnh luã¿ thã¨a vãi sã méˋ thãÝc cû° tûÙnh chäËt tó¯óÀng tÃ£Ý nhó¯ luã¿ thã¨a vãi sã méˋ tÃ£Ý nhiûˆn.

Bû i täÙp minh hãa
CûÂu 1: Cho lû sã thãÝc dó¯óÀng. GiûÀ trã cãÏa biãu thãˋc \(P\, = \,{a^{\frac{2}{3}}}\sqrt a \) bäÝng
Hó¯Ã£ng dä¨n giäÈi
Vãi a >0, ta cû°: \(P\, = \,{a^{\frac{2}{3}}}\sqrt a \, \)\(= \,{a^{\frac{2}{3}}}\,{a^{\frac{1}{2}}}\, = \,{a^{\frac{7}{6}}}\).
CûÂu 2: Rû¤t gãn biãu thãˋc \(P = \frac{{{{\left( {{a^{\sqrt 3 - 1}}} \right)}^{\sqrt 3 + 1}}}}{{{a^{4 - \sqrt 5 }}.{a^{\sqrt 5 - 2}}}}\).
A. P=2
B. P=a2
C. P=1
D. P=a
Hó¯Ã£ng dä¨n giäÈi
Chãn C
Ta cû°:
\(P = \frac{{{{\left( {{a^{\sqrt 3 - 1}}} \right)}^{\sqrt 3 + 1}}}}{{{a^{4 - \sqrt 5 }}.{a^{\sqrt 5 - 2}}}} \)\(= \frac{{{a^{\left( {\sqrt 3 - 1} \right)\left( {\sqrt 3 + 1} \right)}}}}{{{a^{4 - \sqrt 5 + \sqrt 5 - 2}}}} \)\(= \frac{{{a^2}}}{{{a^2}}} = 1\)
Luyãn täÙp Bû i 1 ToûÀn 11 ChûÂn Trãi SûÀng TäÀo
Hãc xong bû i hãc nû y, em cû° thã:
ã NhäÙn biä¢t phûˋp tûÙnh luã¿ thã¨a vãi sã méˋ thãÝc; sã٠dãËng cûÀc tûÙnh chäËt cãÏa phûˋp tûÙnh luã¿ thã¨a trong tûÙnh toûÀn, rû¤t gãn biãu thãˋc tûÙnh giûÀ trã cãÏa biãu thãˋc chãˋa luã¿ thã¨a bäÝng mûÀy tûÙnh cäÏm tay.
ã VäÙn dãËng phûˋp tûÙnh luã¿ thã¨a trong tûÙnh toûÀn, giäÈi quyä¢t cûÀc väËn áã trong cûÀc mûÇn hãc vû trong thãÝc tiã n.
3.1. Trä₤c nghiãm Bû i 1 ToûÀn 11 ChûÂn Trãi SûÀng TäÀo
CûÀc em cû° thã hã thãng läÀi nãi dung kiä¢n thãˋc áûÈ hãc áó¯Ã£Èc thûÇng qua bû i kiãm tra Trä₤c nghiãm ToûÀn 11 ChûÂn trãi sûÀng täÀo Chó¯óÀng 6 Bû i 1 cãÝc hay cû° áûÀp ûÀn vû lãi giäÈi chi tiä¢t.
-
- A. \({{a}^{\frac{2}{3}}}\).
- B. \({{a}^{\frac{3}{4}}}\).
- C. \({{a}^{\frac{4}{3}}}\).
- D. \({{a}^{\frac{3}{2}}}\).
-
- A. a lû cán bäÙc b cãÏa n
- B. b lû cán bäÙc a cãÏa n
- C. a lû cán bäÙc n cãÏa b
- D. b lû cán bäÙc n cãÏa a
-
- A. a < 0
- B. a > 0
- C. a ã R
- D. a ã Z
CûÂu 4-10: Mãi cûÀc em ááng nhäÙp xem tiä¢p nãi dung vû thi thã٠Online áã cãÏng cã kiä¢n thãˋc vã bû i hãc nû y nhûˋ!
3.2. Bû i täÙp SGK Bû i 1 ToûÀn 11 ChûÂn Trãi SûÀng TäÀo
CûÀc em cû° thã xem thûˆm phäÏn hó¯Ã£ng dä¨n GiäÈi bû i täÙp ToûÀn 11 ChûÂn trãi sûÀng täÀo Chó¯óÀng 6 Bû i 1 áã giû¤p cûÀc em nä₤m vã₤ng bû i hãc vû cûÀc phó¯óÀng phûÀp giäÈi bû i täÙp.
HoäÀt áãng khûÀm phûÀ 1 trang 6 SGK ToûÀn 11 ChûÂn trãi sûÀng täÀo täÙp 2 - CTST
ThãÝc hû nh 1 trang 7 SGK ToûÀn 11 ChûÂn trãi sûÀng täÀo täÙp 2 - CTST
VäÙn dãËng 1 trang 7 SGK ToûÀn 11 ChûÂn trãi sûÀng täÀo täÙp 2 - CTST
HoäÀt áãng khûÀm phûÀ 2 trang 7 SGK ToûÀn 11 ChûÂn trãi sûÀng täÀo täÙp 2 - CTST
ThãÝc hû nh 2 trang 9 SGK ToûÀn 11 ChûÂn trãi sûÀng täÀo täÙp 2 - CTST
HoäÀt áãng khûÀm phûÀ 3 trang 9 SGK ToûÀn 11 ChûÂn trãi sûÀng täÀo täÙp 2 - CTST
ThãÝc hû nh 3 trang 10 SGK ToûÀn 11 ChûÂn trãi sûÀng täÀo täÙp 2 - CTST
ThãÝc hû nh 4 trang 10 SGK ToûÀn 11 ChûÂn trãi sûÀng täÀo täÙp 2 - CTST
HoäÀt áãng khûÀm phûÀ 4 trang 10 SGK ToûÀn 11 ChûÂn trãi sûÀng täÀo täÙp 2 - CTST
ThãÝc hû nh 5 trang 11 SGK ToûÀn 11 ChûÂn trãi sûÀng täÀo täÙp 2 - CTST
HoäÀt áãng khûÀm phûÀ 5 trang 11 SGK ToûÀn 11 ChûÂn trãi sûÀng täÀo täÙp 2 - CTST
ThãÝc hû nh 6 trang 12 SGK ToûÀn 11 ChûÂn trãi sûÀng täÀo täÙp 2 - CTST
ThãÝc hû nh 7 trang 12 SGK ToûÀn 11 ChûÂn trãi sûÀng täÀo täÙp 2 - CTST
VäÙn dãËng 2 trang 12 SGK ToûÀn 11 ChûÂn trãi sûÀng täÀo täÙp 2 - CTST
GiäÈi Bû i 1 trang 13 SGK ToûÀn 11 ChûÂn trãi sûÀng täÀo täÙp 2 - CTST
GiäÈi Bû i 2 trang 13 SGK ToûÀn 11 ChûÂn trãi sûÀng täÀo täÙp 2 - CTST
GiäÈi Bû i 3 trang 13 SGK ToûÀn 11 ChûÂn trãi sûÀng täÀo täÙp 2 - CTST
GiäÈi Bû i 4 trang 13 SGK ToûÀn 11 ChûÂn trãi sûÀng täÀo täÙp 2 - CTST
GiäÈi Bû i 5 trang 13 SGK ToûÀn 11 ChûÂn trãi sûÀng täÀo täÙp 2 - CTST
GiäÈi Bû i 6 trang 13 SGK ToûÀn 11 ChûÂn trãi sûÀng täÀo täÙp 2 - CTST
GiäÈi Bû i 7 trang 13 SGK ToûÀn 11 ChûÂn trãi sûÀng täÀo täÙp 2 - CTST
Bû i täÙp 1 trang 7 SBT Toaän 11 TûÂäÈp 2 ChûÂn trãi sûÀng täÀo - CTST
Bû i täÙp 2 trang 8 SBT Toaän 11 TûÂäÈp 2 ChûÂn trãi sûÀng täÀo - CTST
Bû i täÙp 3 trang 8 SBT Toaän 11 TûÂäÈp 1 ChûÂn trãi sûÀng täÀo - CTST
Bû i täÙp 4 trang 8 SBT Toaän 11 TûÂäÈp 2 ChûÂn trãi sûÀng täÀo - CTST
Bû i täÙp 5 trang 8 SBT Toaän 11 TûÂäÈp 2 ChûÂn trãi sûÀng täÀo - CTST
Bû i täÙp 6 trang 8 SBT Toaän 11 TûÂäÈp 2 ChûÂn trãi sûÀng täÀo - CTST
Bû i täÙp 7 trang 8 SBT Toaän 11 TûÂäÈp 2 ChûÂn trãi sûÀng täÀo - CTST
Bû i täÙp 8 trang 9 SBT Toaän 11 TûÂäÈp 2 ChûÂn trãi sûÀng täÀo - CTST
Bû i täÙp 9 trang 9 SBT Toaän 11 TûÂäÈp 2 ChûÂn trãi sûÀng täÀo - CTST
Bû i täÙp 10 trang 9 SBT Toaän 11 TûÂäÈp 2 ChûÂn trãi sûÀng täÀo - CTST
Bû i täÙp 11 trang 9 SBT Toaän 11 TûÂäÈp 2 ChûÂn trãi sûÀng täÀo - CTST
Bû i täÙp 12 trang 9 SBT Toaän 11 TûÂäÈp 2 ChûÂn trãi sûÀng täÀo - CTST
Bû i täÙp 13 trang 9 SBT Toaän 11 TûÂäÈp 2 ChûÂn trãi sûÀng täÀo - CTST
Hãi áûÀp Bû i 1 ToûÀn 11 ChûÂn Trãi SûÀng TäÀo
Trong quûÀ trû˜nh hãc täÙp nä¢u cû° thä₤c mä₤c hay cäÏn trÃ£È giû¤p gû˜ thû˜ cûÀc em hûÈy comment ã mãËc Hãi áûÀp, Cãng áãng ToûÀn hãc HOC247 sä§ hã trÃ£È cho cûÀc em mãt cûÀch nhanh chû°ng!
Chû¤c cûÀc em hãc täÙp tãt vû luûÇn áäÀt thû nh tûÙch cao trong hãc täÙp!
-- Mod ToûÀn Hãc 11 HãC247








