Giải bài 4 trang 22 SBT Toán 10 Chân trời sáng tạo tập 2
Dựa vào đồ thị của hàm số bậc hai được cho, hãy giải các bất phương trình sau:
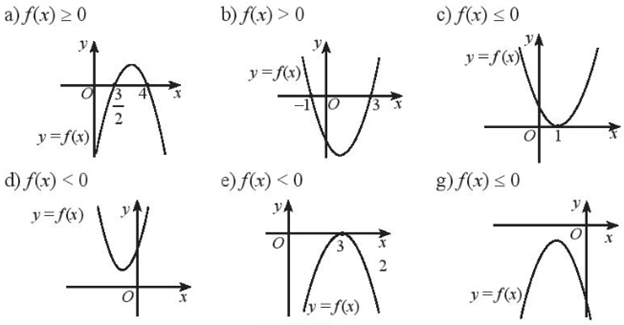
Hướng dẫn giải chi tiết Bài 4
Phương pháp giải
Dựa vào đồ thị ta xác định được nghiệm của bất phương trình
Phần đồ thị nằm trên trục hoành là phần hàm số có giá trị dương
Ngược lại phần đồ thị nằm dưới trục hoành là phần hàm số có giá trị âm
Lời giải chi tiết
a) \(f\left( x \right) \ge 0\) khi và chỉ khi \(x \ge \frac{3}{2}\) và \(x \le 4\)
Vậy tập nghiệm của bất phương trình là \(\left[ {\frac{3}{2};4} \right]\)
b) \(f\left( x \right) > 0\) khi và chỉ khi \(x < - 1\) hoặc \(x > 3\)
Vậy tập nghiệm của bất phương trình là \(\left( { - \infty ; - 1} \right) \cup \left( {3; + \infty } \right)\)
c) \(f\left( x \right) \le 0\) khi và chỉ khi \(x = 1\)
Vậy tập nghiệm của bất phương trình là \(\left\{ 1 \right\}\)
d) \(f\left( x \right) > 0\) với mọi \(x \in \mathbb{R}\). Tập nghiệm của bất phương trình \(f\left( x \right) < 0\) là \(\emptyset \)
e) \(f\left( x \right) < 0\) khi và chỉ khi \(x \ne 3\)
Vậy tập nghiệm của bất phương trình là \(\mathbb{R}\backslash \left\{ 3 \right\}\)
g) \(f\left( x \right) < 0\) với mọi \(x \in \mathbb{R}\). Tập nghiệm của bất phương trình \(f\left( x \right) \le 0\) là \(\mathbb{R}\)
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Giải bài 2 trang 21 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải bài 3 trang 21 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải bài 5 trang 22 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải bài 6 trang 22 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải bài 7 trang 22 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải bài 8 trang 22 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải bài 9 trang 23 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải bài 10 trang 23 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





