Bài 4: Công thức cộng xác suất

Nếu A và B là hai biến cố xung khắc thì:

\(P(A \cup B) = P(A) + P(B)\)   (1.9)

Chứng minh: Ta chứng minh cho trường hợp phép thử có thể phân tích thành n trường hợp đồng khả năng, trong đó có mi trường hợp thuận lợi cho A và m₂ trường hợp thuận lợi cho B. Khi đó số trường hợp thuận lợi cho biến cố \((A \cup B)\) sẽ là: m₁+m₂ (vì A, B là hai biến cố xung khắc).

Ta có thể minh họa số trường hợp thuận lợi như sau:

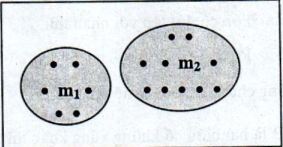
Theo định nghĩa cổ điển ta có: \(P(A \cup B) = \frac{{{m_1} + {m_2}}}{n} = \frac{{{m_1}}}{n} + \frac{{{m_2}}}{n} = P(A) + P(B)\)

Trường hợp tổng quát, công thức trên được phát biểu như sau:

Nếu A₁, A₂,..., A_n là n biến cố xung khắc từng đôi, thì: \(P({A_1} \cup {A_2} \cup ... \cup {A_n}) = P({A_1}) + P({A_2}) + .... + P({A_n})\) (1.10)

Bạn đọc có thể chứng minh công thức trên bằng phương pháp quy nạp.

Thí dụ 1: Một hộp có 10 sản phẩm (trong đó có 2 phế phẩm). Lấy ngẫu nhiên không hoàn lại từ hộp ra 6 sản phẩm. Tìm xác suất để có không quá 1 phế phẩm trong 6 sản phẩm lấy ra.

Giải: Gọi A là biến cố “không có phế phẩm nào trong 6 sản phẩm lấy ra”; B là biến cố “có 1 phế phẩm trong 6 sản phẩm lấy ra” và c là biến cố”có không quá 1 phế phẩm trong 6 sản phẩm lấy ra”.

Ta thấy: 

\(C = A \cup B\)

Mà A, B là hai biến cố xung khắc (vì nó không thể đồng thời xảy ra trong phép thử lấy ngẫu nhiên ra 6 sản phẩm từ hộp). Nên:

\(P(C) = P(A \cup B) = P(A) + P(B)\)

\(P(A) = \frac{{C_8^6}}{{C_{10}^6}} = \frac{{14}}{{105}};\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,P(B) = \frac{{C_2^1.C_8^5}}{{C_{10}^6}} = \frac{{56}}{{105}}\)

Vậy

\(P(C) = \frac{{14}}{{105}} + \frac{{56}}{{105}} = \frac{{70}}{{105}} = \frac{2}{3}\)

Từ định lý trên ta có thể suy ra hệ quả sau:

Hệ quả: Nếu A và \(\overline A \) là hai biến cố đối lập với nhau thì:  \(P(A) = 1 - P(\overline A )\) (1.11)

Bạn đọc có thể dễ dàng chứng minh các hệ quả trên.

Nếu A và B là hai biến cố không xung khắc thì: \(P(A \cup B) = P(A) + P(B) - P(AB)\)            (1.12)

Chứng minh: Giả sử phép thử có n trường hợp đồng khả năng, trong đó có m₁ trường hợp thuận lợi cho A, m₂ trường hợp thuận lợi cho B. Vì A, B không xung khắc nên nói chung sẽ có k trường hợp thuận lợi cho cả A và B. Khi đó số trường hợp thuận lợi cho biến cố \((A \cup B)\) sẽ là \({m_1} + {m_2} - k\)

Ta có thể minh họa trường hợp này như sau:

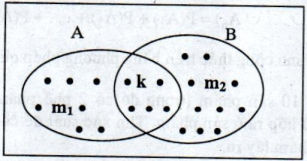
Theo mô tả ở hình trên mỗi nốt chấm đen là một trường hợp thuận lợi thì: m₁ = 12; m₂ = 15; k = 5

Theo định nghĩa cổ điển của xác suất, ta có:

\(P(A \cup B) = \frac{{{m_1} + {m_2} - k}}{n} = \frac{{{m_1}}}{n} + \frac{{{m_2}}}{n} - \frac{k}{n} = P(A) + P(B) - P(AB)\)

vì:                \(\frac{{{m_1}}}{n} = P(A);\,\,\frac{{{m_2}}}{n} = P(B);\,\,\frac{k}{n} = P(AB)\)

Thí dụ: Một lớp có 50 sinh viên, trong đó có 20 sinh viên học giỏi Toán; 30 sinh viên học giỏi Anh văn; 10 sinh viên học giỏi cả hai môn Toán và Anh văn. Chọn ngẫu nhiên một sinh viên của lớp. Tun xác suất để chọn được sinh viên học giỏi ít nhất một môn trong hai môn Toán và Anh văn.

Giải: Gọi A là biến cố chọn được sinh viên học giỏi môn Toán; B là biến cố chọn được sinh viên học giỏi môn Anh văn; c là biến cô' chọn được sinh viên học giỏi ít nhất một trong hai môn Toán và Anh văn. Ta có:

\(C = A \cup B\)

A, B là hai biến cố không xung khắc (vì A và B có thể xảy ra đồng thời trong cùng một phép thử. Đó chính là trường hợp chọn được một sinh viên học giỏi cả hai môn Toán và Anh văn).

Do đó: 

\(P(C) = P(A) + P(B) - P(AB) = \frac{{20}}{{50}} + \frac{{30}}{{50}} - \frac{{10}}{{50}} = \frac{{40}}{{50}} = 0,8\)

Trường hợp tổng quát công thức trên được phát biểu như sau:

Nếu A₁, A₂,..., A_n là n biến cố không xung khắc thì:

\(P({A_1} \cup {A_2} \cup ... \cup {A_n}) = \sum\limits_{i = 1}^n {P({A_i})} - \sum\limits_{i < j} {P({A_i}{A_j}} ) + \sum\limits_{i < j < k} {({A_i}{A_j}{A_k})} .... + {( - 1)^{n - 1}}P({A_1}.{A_2}...{A_n})\)  (1.13)

Trường hợp n = 3:

\(P({A_1} \cup {A_2} \cup {A_3}) = P({A_1}) + P({A_2}) + P({A_3}) - P({A_1}{A_2}) - P({A_1}{A_3}) - P({A_2}{A_3}) + P({A_1}{A_2}{A_3})\) (1.14)

Trường hợp n = 4:

\(\begin{array}{l} P({A_1} \cup {A_2} \cup {A_3} \cup {A_4}) = P({A_1}) + P({A_2}) + P({A_3}) + P({A_4})\\ - P({A_1}{A_2}) - P({A_1}{A_3}) - P({A_1}{A_4}) - P({A_2}{A_3}) - P({A_2}{A_4})\\ - P({A_3}{A_4}) + P({A_1}{A_2}{A_3}) + P({A_1}{A_2}{A_4}) + P({A_1}{A_3}{A_4})\\ + P({A_2}{A_3}{A_4}) - P({A_1}{A_2}{A_3}{A_4}) \end{array}\) (1.15)