-
Câu hỏi:
Trong mặt phẳng tọa độ Oxy, cho đường tròn lượng giác. M thuộc đường tròn sao cho \(\widehat{AOM}=\frac{\pi }{6}\) (M thuộc góc phần tư thứ tư). Số đo \(\overset{\curvearrowright }{\mathop{AM}}\,\) có thể là giá trị nào sau đây?
-
A.
\(\frac{5\pi }{6}\)
-
B.
\(\frac{\pi }{6}\)
-
C.
\(\frac{-13\pi }{6}\)
-
D.
\(\frac{-11\pi }{6}\)
Lời giải tham khảo:
Đáp án đúng: C
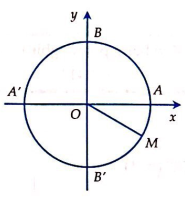
Vì M thuộc góc phần tư thứ IV và \(\widehat{AOM}=30{}^\circ \) nên đây là góc tính theo chiều âm
\(\Rightarrow \widehat{AOM}=\alpha \) theo chiều dương là \(\alpha =2\pi -\frac{\pi }{6}+k2\pi \left( k\in \mathbb{Z} \right)\)
\(\alpha =\frac{11\pi }{6}+k2\pi \left( k\in \mathbb{Z} \right)\)
\(\Rightarrow \) sđ \(\overset{\curvearrowright }{\mathop{AM}}\,=\frac{11\pi }{6}+k2\pi \left( k\in \mathbb{Z} \right)\)
Vì \(k\in \mathbb{Z}\) nên chỉ có đáp án C thỏa mãn (với \(k=-2\)).
Đáp án C.
Hãy trả lời câu hỏi trước khi xem đáp án và lời giải -
A.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
CÂU HỎI KHÁC
- Một đường tròn có bán kính \(R=10cm\). Tìm số đo (rad) của cung có độ dài là 5cm.
- Cho đường tròn \(\left( O;R \right)\) ngoại tiếp lục giác đều ABCDEF.
- Trong mặt phẳng tọa độ Oxy, cho đường tròn lượng giác. M thuộc đường tròn sao cho \(\widehat{AOM}=\frac{\pi }{6}\)
- Cho bốn cung (trên một đường tròn định hướng): \(\alpha =\frac{\pi }{3};\beta =\frac{10\pi }{3}\);
- Đổi số đo cung sau sang radian: \(70{}^\circ \) (làm tròn đến hàng phần nghìn).
- Đổi số đo cung sau sang độ, phút, giây: \(\frac{5}{6}\text{rad}\).
- Trên đường tròn lượng giác, cho cung lượng giác \(s\overset{\curvearrowright }{\mathop{AM}}\,\)
- Chọn điểm \(A\left( 1;0 \right)\) làm điểm đầu cung lượng giác trên đường tròn lượng giác.
- Một đường tròn bán kính 20cm. Tính độ dài cung trên đường tròn có số đo \(\frac{\pi }{16}\)
- Khi biểu diễn cung lượng giác trên đường tròn trên lượng giác. Khẳng định nào dưới đây là sai?




