-
Câu hỏi:
Cho tứ diện ABCD. Gọi M,N lần lượt là trung điểm các cạnh AB và AC, E là điểm trên cạnh CD với ED=3EC. Thiết diện tạo bởi mặt phẳng (MNE) và tứ diện ABCD là:
-
A.
Tam giác MNE
-
B.
Tứ giác MNEF với F là điểm bất kì trên cạnh BD
-
C.
Hình bình hành MNEF với F là điểm trên cạnh BD mà EF // BC
-
D.
Hình thang MNEF với F là điểm trên cạnh BD mà EF // BC
Lời giải tham khảo:
Đáp án đúng: D
Đáp án: D
Giải thích:
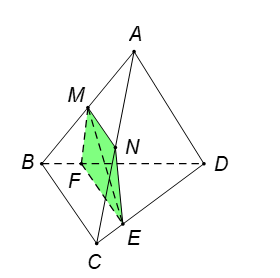
Tam giác ABC có M,N lần lượt là trung điểm của AB, AC
Suy ra MN là đường trung bình của tam giác ABC⇒MN // BC
Từ E kẻ đường thẳng d song song với BC và cắt BD tại F⇒EF // BC
Do đó MN // EF suy ra bốn điểm M, N, E, F đồng phẳng và MNEF là hình thang.
Vậy hình thang MNEF là thiết diện cần tìm.
Hãy trả lời câu hỏi trước khi xem đáp án và lời giải -
A.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
CÂU HỎI KHÁC
- Trong các khẳng định sau, khẳng định nào đúng? Qua 2 điểm phân biệt có duy nhất một mặt phẳng; ...
- Trong không gian, cho 4 điểm không đồng phẳng. Có thể xác định được bao nhiêu mặt phẳng phân biệt từ các điểm đã cho?
- Cho tứ diện ABCD. Gọi E, F, G là các điểm lần lượt thuộc các cạnh AB, AC, BD sao cho EF cắt BC tại I, EG cắt AD tại H. Ba đường thẳng nào sau đây đồng quy?
- Các yếu tố nào sau đây xác định một mặt phẳng duy nhất?
- Trong các mệnh đề sau đây, mệnh đề nào sai? Hai mặt phẳng có một điểm chung thì chúng có vô số điểm chung khác nữa
- Cho 3 đường thẳng \(d_1,d_2,d_3\) không cùng thuộc một mặt phẳng và cắt nhau từng đôi. Khẳng định nào sau đây đúng?
- Thiết diện của 1 tứ diện có thể là:
- Cho tứ diện ABCD. Gọi M,N lần lượt là trung điểm các cạnh AB và AC, E là điểm trên cạnh CD với ED=3EC. Thiết diện tạo bởi mặt phẳng (MNE) và tứ diện ABCD là:
- Cho tứ diện ABCD. Gọi H, K lần lượt là trung điểm các cạnh AB, BC. Trên đường thẳng CD lấy điểm M nằm ngoài đoạn CD. Thiết diện của tứ diện với mặt phẳng (HKM) là:
- Cho 3 điểm không thẳng hàng. số mặt phẳng phân biệt đi qua ba điểm đó là:

