-
Câu hỏi:
Cho hình chóp S.ABC có đáy ABC là tam giác đều, SA⊥(ABC). Gọi (P) là mặt phẳng qua B và vuông góc với SC. Thiết diện của (P) và hình chóp S.ABC là:
-
A.
Hình thang vuông.
-
B.
Tam giác đều.
-
C.
Tam giác cân.
-
D.
Tam giác vuông.
Lời giải tham khảo:
Đáp án đúng: D
Đáp án: D
Giải thích:
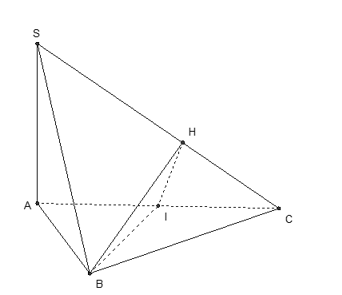
Gọi I là trung điểm của AC, kẻ IH⊥SC
Ta có BI⊥AC,BI⊥SA
⇒BI⊥SC.
Do đó SC⊥(BIH) hay thiết diện là tam giác BIH.
Mà BI⊥(SAC) nên BI⊥IH hay thiết diện là tam giác vuông.
Hãy trả lời câu hỏi trước khi xem đáp án và lời giải -
A.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
CÂU HỎI KHÁC
- Cho hai đường thẳng phân biệt a,b và mặt phẳng (P), trong đó
- Khẳng định nào sau đây sai? Nếu đường thẳng d⊥(α) thì d vuông góc với hai đường thẳng trong (α).
- Trong không gian cho đường thẳng Δ và điểm O. Qua O có
- Trong không gian tập hợp các điểm M cách đều hai điểm cố định A và B là
- Cho a,b,c là các đường thẳng trong không gian. Tìm mệnh đề sai trong các mệnh đề sau.
- Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA⊥(ABCD).
- Cho hình chóp S.ABC có cạnh SA⊥(ABC) và đáy ABC là tam giác cân ở C
- Cho tứ diện ABCD. Vẽ AH⊥(BCD)
- Cho hình chóp S.ABC có đáy ABC là tam giác đều, SA⊥(ABC)
- Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, cạnh bên SA⊥(ABC)
VIDEO
YOMEDIA
ADMICRO
