Hướng dẫn Giải bài tập Toán 6 Chân trời sáng tạo Bài tập cuối chương 3 Bài tập cuối chương 3 giúp các em học sinh nắm vững phương pháp giải bài tập và ôn luyện tốt kiến thức.
-
Giải câu 1 trang 93 SGK Toán 6 Chân trời sáng tạo tập 1 - CTST
Hình thoi có độ dài hai đường chéo lần lượt là 50 m và 60 m thì diện tích là:
(A) 300 m2.
(B) 3 000 m2.
(C) 1 500 m2.
(D) 150 m2.
-
Giải câu 2 trang 93 SGK Toán 6 Chân trời sáng tạo tập 1 - CTST
Hình thang cân có độ dài cạnh đáy và chiều cao lần lượt là 40 m, 30 m, 25 m, có diện tích là:
(A) 1 750 m2.
(B) 175 m2.
(C) 875 m2.
(D) 8 750 m2.
-
Giải câu 3 trang 93 SGK Toán 6 Chân trời sáng tạo tập 1 - CTST
Hình bình hành có chiều dài một cạnh và chiều cao lần lượt là 70 dm và 50 dm có diện tích là:
(A) 35 m2.
(B) 3 500 m2.
(C) 17,5 m2.
(D) 350 m2.
-
Giải bài 1 trang 93 SGK Toán 6 Chân trời sáng tạo tập 1 - CTST
Em hãy vẽ các hình sau đây:
a) Tam giác đều có cạnh là 5 cm.
b) Hình chữ nhật có chiều dài 5 cm và chiều rộng 3 cm.
c) Hình vuông có cạnh 3 cm.
d) Hình bình hành có hai cạnh liên tiếp là 6 cm, 8 cm và chiều cao bằng 4 cm.
e) Hình thoi có cạnh dài 5 cm.
- VIDEOYOMEDIA
-
Giải bài 2 trang 93 SGK Toán 6 Chân trời sáng tạo tập 1 - CTST
Hãy cắt 3 hình như hình dưới đây và ghép lại để được một hình vuông.

-
Giải bài 3 trang 93 SGK Toán 6 Chân trời sáng tạo tập 1 - CTST
Hình dưới đây gồm các hình nào?

-
Giải bài 4 trang 93 SGK Toán 6 Chân trời sáng tạo tập 1 - CTST
Hãy cắt ghép 5 hình bình hành sao cho khi ghép lại tạo thành một hình bình hành
-
Giải bài 5 trang 93 SGK Toán 6 Chân trời sáng tạo tập 1 - CTST
Hãy đếm xem hình dưới đây có bao nhiêu hình thang cân, bao nhiêu hình lục giác đều?
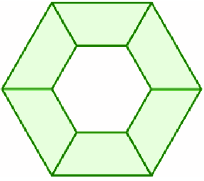
-
Giải bài 6 trang 93 SGK Toán 6 Chân trời sáng tạo tập 1 - CTST
Hãy cắt 6 hình tam giác đều rồi ghép lại thành hình bình hành.
-
Giải bài 7 trang 93 SGK Toán 6 Chân trời sáng tạo tập 1 - CTST
Để làm một con diều, bạn Nam lấy một tờ giấy hình chữ nhật có chiều dài 60 cm, chiều rộng 40 cm để cắt thành một hình thoi như hình bên dưới. Hãy tính diện tích của con diều.

-
Giải bài 1 trang 76 SBT Toán 6 Chân trời sáng tạo tập 1 - CTST
Cho hình vuông ABCD có AB = 9 cm. Tính độ dài các đoạn thẳng DC và AD.
-
Giải bài 2 trang 76 SBT Toán 6 Chân trời sáng tạo tập 1 - CTST
Dùng thước và eke để vẽ hình vuông có độ dài cạnh 7 cm. Hãy dùng compa so sánh đường chèo của hình vuông đó.
-
Giải bài 3 trang 76 SBT Toán 6 Chân trời sáng tạo tập 1 - CTST
Cho tam giác đều DEF có DE = 5 cm. Tính độ dài các cạnh EF, DF.
-
Giải bài 4 trang 76 SBT Toán 6 Chân trời sáng tạo tập 1 - CTST
Dùng thước và compa để vẽ tam giác đều có độ dài cạnh 3 cm.
-
Giải bài 5 trang 77 SBT Toán 6 Chân trời sáng tạo tập 1 - CTST
Cho lục giác đều ABCDEF với cạnh AB = 8 cm và đường chéo AD = 16 cm. Tính độ dài các doạn thẳng CD và CF.
-
Giải bài 6 trang 77 SBT Toán 6 Chân trời sáng tạo tập 1 - CTST
Cho hình chữ nhật ABCD có AB = 12 cm, BC = 9 cm, BD = 15 cm. Tính độ dài của AD, CD, AC.
-
Giải bài 7 trang 77 SBT Toán 6 Chân trời sáng tạo tập 1 - CTST
Cho hình thoi ABCD với O là giao điểm của hai đường chéo. Biết AB = 20 cm, OA = 16 cm, OB = 12 cm. Tính độ dài các cạnh và các đường chéo của hình thoi.
-
Giải bài 8 trang 77 SBT Toán 6 Chân trời sáng tạo tập 1 - CTST
Cho hình bình hành ABCD có O là giao điểm của hai đường chéo và thỏa mãn AB = 16 cm, AD = 10 cm, OC = 6 cm. Tính độ dài của CD, BC, AC.
-
Giải bài 9 trang 77 SBT Toán 6 Chân trời sáng tạo tập 1 - CTST
Cho hình thang cân MNPQ với cạnh đáy là MN và PQ, PN = 6 cm, PM = 10 cm. Tính MQ, NQ.
-
Giải bài 10 trang 77 SBT Toán 6 Chân trời sáng tạo tập 1 - CTST
Tính chu vi và diện tích của hình bình hành ABCD (như hình bên). Biết rằng AD = 6 cm; AB = 10 cm, DH = 9cm.
-
Giải bài 11 trang 77 SBT Toán 6 Chân trời sáng tạo tập 1 - CTST
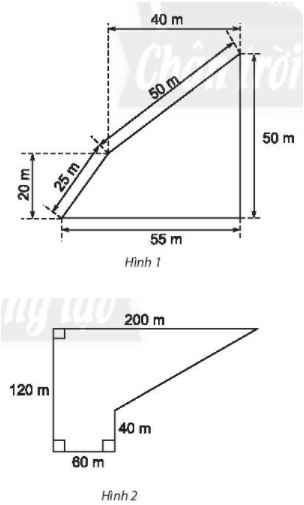
Tính chu vi và diện tích của Hình 1 và tính diện tích của Hình 2 sau đây.
-
Giải bài 12 trang 78 SBT Toán 6 Chân trời sáng tạo tập 1 - CTST
Tính chu vi và diện tích của hồ bơi có kích thước như hình vẽ sau:
-
Giải bài 13 trang 78 SBT Toán 6 Chân trời sáng tạo tập 1 - CTST
Tính diện tích của hình sau:
-
Giải bài 14 trang 78 SBT Toán 6 Chân trời sáng tạo tập 1 - CTST
Tính diện tích của hình sau:






.JPG)
.JPG)
.JPG)
