Luyện tập 1 trang 30 SGK Toán 11 Kết nối tri thức tập 2
Cho tam giác MNP vuông tại N và một điểm A nằm ngoài mặt phẳng (MNP). Lần lượt lấy các điểm B, C, D sao cho M, N, P tương ứng là trung điểm của AB, AC, CD (H.7.7). Chứng minh rằng AD và BC vuông góc với nhau và chéo nhau.
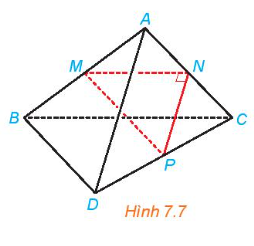
Hướng dẫn giải chi tiết Luyện tập 1
Phương pháp giải
HS sử dụng tính chất:
Nếu \(a//b,\) \( a\bot c \Rightarrow b\bot c\).
Lời giải chi tiết
Ta biết rằng tam giác MNP là tam giác vuông tại N, do đó ta có:
\(MN^{2}+NP^{2}=MP^{2}\)
Theo giả thiết, M, N, P lần lượt là trung điểm của AB, AC và CD, nên ta có:
\(MN=\frac{1}{2} AB\)
\(NP=\frac{1}{2} AC =\frac{1}{2} CD\)
Thay các giá trị này vào công thức trên, ta có:
\((\frac{1}{2} AB)^{2} + (\frac{1}{2} AC)^{2}=(\frac{1}{2}CD)^{2}\)
\(\Rightarrow AB^{2}+AC^{2}=CD^{2}\)
Như tam giác ABC và tam giác CDA là hai tam giác vuông cân có đỉnh C và D lần lượt là các đỉnh vuông góc
Gọi H là trung điểm của đoạn thẳng AB. Khi đó, ta có:
NH là đường trung trực của đoạn thẳng AB
DH là đường trung trực của đoạn thẳng CD
Do đó, ta có thể kết luận rằng đường NH và đường DH cắt nhau tại một điểm O, và O là trung điểm của đoạn thẳng BC. Vậy ta đã chứng minh rằng AD và BC chéo nhau.
Vì NH là đường trung trực của đoạn thẳng AB, nên NH vuông góc với AB. Tương tự, DH vuông góc với CD và BC vuông góc với NH. Do đó, ta có thể kết luận rằng AD và BC vuông góc với nhau.
-- Mod Toán 11 HỌC247
Bài tập SGK khác
Vận dụng trang 29 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Hoạt động 2 trang 29 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Giải Bài 7.1 trang 30 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Giải Bài 7.2 trang 30 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Giải Bài 7.3 trang 30 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Giải Bài 7.4 trang 30 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Bài tập 7.1 trang 25 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Bài tập 7.2 trang 26 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Bài tập 7.3 trang 26 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Bài tập 7.4 trang 26 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Bài tập 7.5 trang 26 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





