Bài tập 7.4 trang 26 SBT Toán 11 Tập 2 Kết nối tri thức
Cho hình chóp \(S.ABCD\) có đáy là hình vuông tâm \(O\) và tất cả các cạnh của hình chóp đều bằng a. Gọi \(M\), N lần lượt là trung điểm các cạnh \(SA,~AB\).
a) Tính góc giữa các cặp đường thẳng sau: \(MN\) và \(SD;~MO\) và \(SB\).
b) Tính tan của góc giữa hai đường thẳng \(SN\) và \(BC\).
Hướng dẫn giải chi tiết Bài 7.4
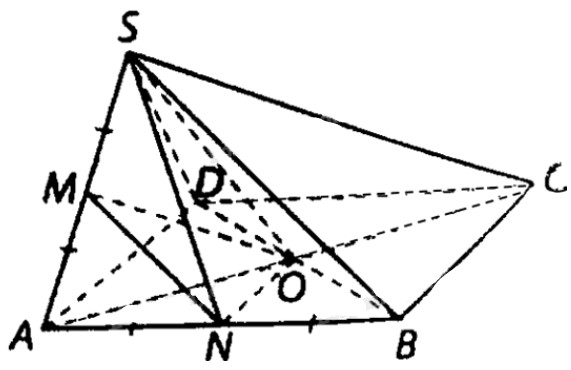
a) Ta có: \(B{D^2} = S{B^2} + S{D^2} = 2{a^2}\) nên \(\Delta SBD\) vuông tại \(S\), mà \(MN//SB\).
Suy ra \(\left( {MN,SD} \right) = \left( {SB,SD} \right) = {90^ \circ }\).
Với O là giao điểm của \(AC\) và \(BD\) thì \(MO//SC\).
Khi đó \(\left( {MO,SB} \right) = \left( {SC,SB} \right) = \widehat {BSC} = {60^ \circ }\).
b) Vì \(ON{\rm{ }}//BC\) nên \(\left( {SN,BC} \right) = \left( {SN,ON} \right) = \widehat {SNO}\).
Ta có \(SO = \frac{{a\sqrt 2 }}{2}; ON = \frac{a}{2}\) và tam giác \(SNO\) vuông tại O nên \({\rm{tan}}\widehat {SNO} = \frac{{SO}}{{ON}} = \sqrt 2 \).
Vậy \({\rm{tan}}\left( {SN,BC} \right) = \sqrt 2 \).
-- Mod Toán 11 HỌC247
Bài tập SGK khác
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





