Bài tập 29 trang 117 SGK Hình học 11 NC
Cho tứ diện ABCD có AC = BC = AD = BD = a, AB = c, CD = c’. Tính khoảng cách giữa hai đường thẳng AB và CD.
Hướng dẫn giải chi tiết
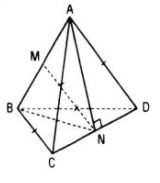
Gọi M, N lần lượt là trung điểm của AB và CD
ΔACD cân nên AN ⊥ CD và ΔBCD cân nên BN ⊥ CD.
Do đó CD ⊥ (ABN) suy ra CD ⊥ MN.
Tương tự ta cũng có AB ⊥ MN
Vậy d(AB, CD) = MN
Ta có:
\(\begin{array}{*{20}{l}}
\begin{array}{l}
M{N^2} = A{N^2} - A{M^2}\\
= A{D^2} - N{D^2} - A{M^2}
\end{array}\\
\begin{array}{l}
= {a^2} - \frac{{c{\prime ^2}}}{4} - \frac{{{c^2}}}{4}\\
= \frac{1}{4}(4{a^2} - c{\prime ^2} - {c^2})
\end{array}
\end{array}\)
Vậy \(MN = \frac{1}{2}\sqrt {4{a^2} - c{\prime ^2} - {c^2}} \)
với điều kiện \(4{a^2} > {c^2} + c{\prime ^2}\)
-- Mod Toán 11 HỌC247
Bài tập SGK khác
-


Tính hoảng cách từ A đến mp(MNP) biết AB=a, AD=2a, AA’=3a
bởi Gọi Em
 18/10/2017
18/10/2017
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB=a, AD=2a, AA’=3a.Gọi M,N,P lần lượt
là trung điểm của BC, C’D’ và DD’.Tính khoảng cách từ A đến mp(MNP)?Theo dõi (0) 1 Trả lời -


Tính khoảng cách giữa 2 đt chéo nhau AB và CA' biết ABCD.A'B'C'D' là hình lập phương cạnh a
bởi Tam Thiên
 17/08/2017
17/08/2017
Hình lập phương ABCDA'B'C'D' cạnh a. Tính :
a,d(AB;CA')
B,d(AB';B'C')
C,d(AC';A'D)
Theo dõi (1) 1 Trả lời -


Hình lăng trụ đều ABCA'B'C' AB=AA'=a.Tính :
a,d(AB,CC')
b,d(AB;BC')
c,d(AM;BC').M là trung điểm của BC
Theo dõi (1) 0 Trả lời -


Cho hình lăng trụ ABCA'B'C' . AB'=2a=BC'=A'B.Tam giác ABC đều cạnh a.
Tính :a,d(AB:CC')
b,d(AB;BC')
Theo dõi (1) 0 Trả lời -
ADMICRO


Cho hình chóp S,ABCD có đáy là hình vuông cạnh a, SD= \(\frac{a\sqrt{17}}{2}\) , hình chiếu vuông góc H của S lên mp(ABCD) là trung điểm AB. Gọi K là trung điểm AD. Khoảng cách giữa hai đường SD và HK theo a?
Theo dõi (0) 1 Trả lời


