Bài tập 33 trang 118 SGK Hình học 11 NC
Cho hình hộp thoi ABCD.A’B’C’D’ có các cạnh đều bằng a và \(\widehat {BAD} = \widehat {BAA\prime } = \widehat {DAA\prime } = {60^0}\). Tính khoảng cách giữa hai mặt phẳng đáy (ABCD) và (A’B’C’D’)
Hướng dẫn giải chi tiết
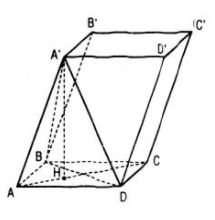
Từ giả thiết suy ra các tam giác A’AD, BAD, A’AB là các tam giác cân cùng có góc ở đỉnh bằng 600 nên chúng là các tam giác đều. Như vậy tứ diện A’ABD có các cạnh cùng bằng a hay A’ABD là tứ diện đều. Khi đó hình chiếu của A’ trên mp(ABCD) chính là trọng tâm H của tam giác đều ABD. Khoảng cách giữa hai mặt phẳng đáy (ABCD) và (A’B’C’D’) chính là độ dài A’H. Ta có:
\(\begin{array}{l}
A\prime {H^2} = AA{\prime ^2} - A{H^2}\\
= {a^2} - {\left( {\frac{{a\sqrt 3 }}{3}} \right)^2} = {a^2} - \frac{{{a^2}}}{3} = \frac{{2{a^2}}}{3}
\end{array}\)
Vậy \(A\prime H = \frac{{a\sqrt 6 }}{3}\)
-- Mod Toán 11 HỌC247
Bài tập SGK khác
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.


