Giải bài 2.1 tr 63 SBT Hình học 11
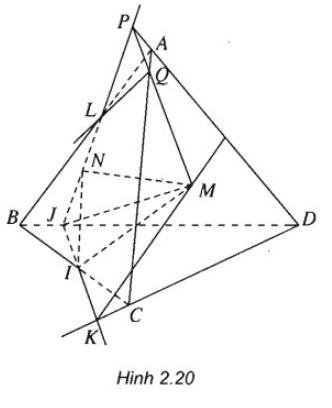
Cho tứ diện ABCD và điểm M thuộc miền trong của tam giác ACD. Gọi I và J tương ứng là hai điểm trên cạnh BC và BD sao cho IJ không song song với CD
a) Hãy xác định giao tuyến của hai mặt phẳng (IJM) và (ACD).
b) Lấy N là điểm thuộc miền trong của tam giác ABD sao cho JN cắt đoạn AB tại L. Tìm giao tuyến của hai mặt phẳng (MNJ) và (ABC)
Hướng dẫn giải chi tiết
a) Nhận xét:
Do giả thiết cho IJ không song song với CD và chúng cùng nằm trong mặt phẳng (BCD) nên khi kéo dài chúng gặp nhau tại một điểm.
Gọi K = IJ ∩ CD.
Ta có: M là điểm chung thứ nhất của (ACD) và (IJM);
\(\left\{ \begin{array}{l}
K \in IJ\\
IJ \subset \left( {MIJ} \right)
\end{array} \right. \Rightarrow K \in \left( {MIJ} \right)\) và \(\left\{ \begin{array}{l}
K \in CD\\
CD \subset \left( {ACD} \right)
\end{array} \right. \Rightarrow K \in \left( {ACD} \right)\)
Vậy (MIJ) ∩ (ACD) = MK
b) Với L = JN ∩ AB ta có:
\(\begin{array}{l}
\left\{ \begin{array}{l}
L \in JN\\
JN \subset \left( {MNJ} \right)
\end{array} \right. \Rightarrow L \in \left( {MNJ} \right)\\
\left\{ \begin{array}{l}
L \in AB\\
AB \subset \left( {ABC} \right)
\end{array} \right. \Rightarrow L \in \left( {ABC} \right)
\end{array}\)
Như vậy L là điểm chung thứ nhất của hai mặt phẳng (MNJ) và (ABC)
Gọi P = JL ∩ AD, Q = PM ∩ AC
Ta có:
\(\begin{array}{l}
\left\{ \begin{array}{l}
Q \in PM\\
PM \subset \left( {MNP} \right)
\end{array} \right. \Rightarrow Q \in \left( {MNJ} \right)\\
\left\{ \begin{array}{l}
Q \in AC\\
AC \subset \left( {ABC} \right)
\end{array} \right. \Rightarrow Q \in \left( {ABC} \right)
\end{array}\)
Nên Q là điểm chung thứ hai của (MNJ) và (ABC)
Vậy LQ = (ABC) ∩ (MNJ).
-- Mod Toán 11 HỌC247
Bài tập SGK khác
Bài tập 9 trang 54 SGK Hình học 11
Bài tập 10 trang 54 SGK Hình học 11
Bài tập 2.2 trang 63 SBT Hình học 11
Bài tập 2.3 trang 63 SBT Hình học 11
Bài tập 2.4 trang 63 SBT Hình học 11
Bài tập 2.5 trang 64 SBT Hình học 11
Bài tập 2.6 trang 64 SBT Hình học 11
Bài tập 2.7 trang 64 SBT Hình học 11
Bài tập 2.8 trang 64 SBT Hình học 11
Bài tập 2.9 trang 64 SBT Hình học 11
Bài tập 1 trang 49 SGK Hình học 11 NC
Bài tập 2 trang 50 SGK Hình học 11 NC
Bài tập 3 trang 50 SGK Hình học 11 NC
Bài tập 4 trang 50 SGK Hình học 11 NC
Bài tập 5 trang 50 SGK Hình học 11 NC
Bài tập 6 trang 50 SGK Hình học 11 NC
Bài tập 7 trang 50 SGK Hình học 11 NC
Bài tập 8 trang 50 SGK Hình học 11 NC
Bài tập 9 trang 50 SGK Hình học 11 NC
Bài tập 10 trang 50 SGK Hình học 11 NC
Bài tập 11 trang 50 SGK Hình học 11 NC
Bài tập 12 trang 51 SGK Hình học 11 NC
Bài tập 13 trang 51 SGK Hình học 11 NC
Bài tập 14 trang 51 SGK Hình học 11 NC
-


Cho hình chóp S.ABCD, các điểm A’, B’, C’ lần lượt thuộc các cạnh SA, SB, SC. Phát biểu nào sau đây là đúng?
bởi Long lanh
 22/01/2021
22/01/2021
A. Thiết diện của (A’B’C’) với hình chóp S.ABCD là tam giác A’B’C’
B. Thiết diện của (A’B’C’) với hình chóp S.ABCD là tứ giác A’B’C’D’ với D’ là giao điểm của B’I với SD, trong đó I là giao điểm của A’C’ với SO, O là giao điểm của AC và BD
C. Thiết diện của (A’B’C’) với hình chóp S.ABCD là tứ giác SA’B’C’
D. Thiết diện của (A’B’C’) với hình chóp S.ABCD là tứ giác A’B’C’D
Theo dõi (0) 1 Trả lời -


Cho hình chóp S.ABCD, M là điểm nằm trong tam giác SAD. Phát biểu nào sau đây là đúng?
bởi can tu
 21/01/2021
21/01/2021
A. Giao điểm của (SMC) với BD là giao điểm của CN với BD, trong đó N là giao điểm của SM và AD.
B. Giao điểm của (SAC) với BD là giao điểm của SA và BD
C. Giao điểm của (SAB) với CM là giao điểm của SA và CM
D. Đường thẳng DM không cắt mặt phẳng (SBC)
Theo dõi (0) 1 Trả lời