Bài tập 19 trang 114 SGK Toán 11 NC
Chứng minh rằng mỗi dãy số sau là một cấp số cộng và hãy xác định công sai của cấp số cộng đó:
a. Dãy số (un) với un = 19n–5;
b. Dãy số (un) với un = an+b, trong đó a và b là các hằng số.
Hướng dẫn giải chi tiết
a) Ta có:
un+1 − un = 19(n+1)−5−(19n−5) = 19 với mọi n ≥ 1.
Do đó (un) là một cấp số cộng với công sai d = 19.
b) Ta có:
un+1 − un = a(n+1)+b−(an+b) = a với mọi n ≥ 1.
Do đó (un) là một cấp số cộng với công sai d = a.
-- Mod Toán 11 HỌC247
Bài tập SGK khác
-


Giải phương trình sin^2 x-2sinx-3=0
bởi Nguyễn Thu Phương
 25/12/2019
Cấp số cộng
25/12/2019
Cấp số cộng Theo dõi (1) 2 Trả lời
Theo dõi (1) 2 Trả lời -


Nếu dãy 1/(b+c), 1/(c+a), 1/(a+b) lập thành cấp số cộng thì dãy nào sau đây lập thành cấp số cộng?
bởi Vũ Đức Đại
 20/12/2019
Câu 32 ấy ạ
20/12/2019
Câu 32 ấy ạ Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Nếu 1/b+c,1/c+a, 1/a+b lập thành một cấp số cộng thì dãy số nào sau đây lập thành một cấp số cộng?
bởi Vũ Đức Đại
 20/12/2019
Nếu 1b c;1c a;1a b1b c;1c a;1a b lập thành một cấp số cộng (theo thứ tự đó) thì dãy số nào sau đây lập thành một cấp số cộngTheo dõi (0) 0 Trả lời
20/12/2019
Nếu 1b c;1c a;1a b1b c;1c a;1a b lập thành một cấp số cộng (theo thứ tự đó) thì dãy số nào sau đây lập thành một cấp số cộngTheo dõi (0) 0 Trả lời -


Tìm u1, d biết un là cấp số cộng có u5=7, u9=23
bởi Ly Trần Hải
 19/12/2019
Cho(Un) là cấp số cộg,U5=7,U9=23
19/12/2019
Cho(Un) là cấp số cộg,U5=7,U9=23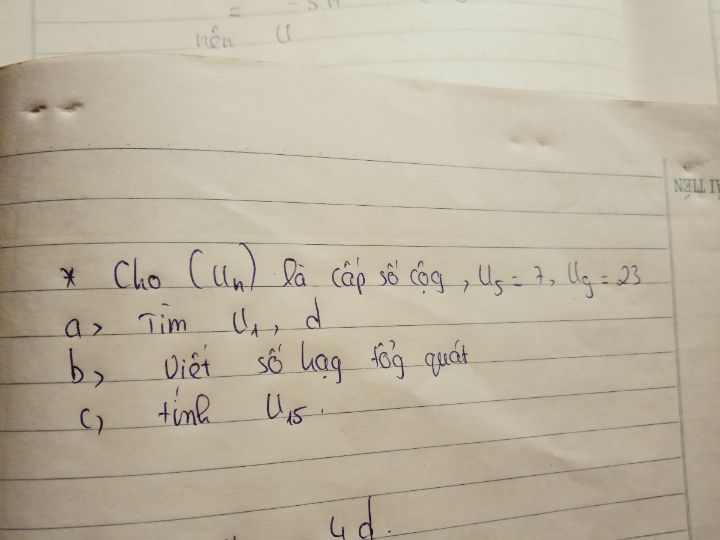 Theo dõi (1) 3 Trả lời
Theo dõi (1) 3 Trả lời -
ADMICRO

 Câu 38
Câu 38 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Xét dãy các số tự nhiên lẽ số 2017 là số hạng thứ mấy?
bởi Tú Nguyễn
 18/12/2019
18/12/2019
 Theo dõi (1) 1 Trả lời
Theo dõi (1) 1 Trả lời -


 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời


