Mời các bạn cùng tham khảo nội dung bài giảng Bài 4: Tính xác suất sai lầm loại 2 sau đây để tìm hiểu về xác suất sai lầm loại 2 với ví dụ chứng minh cụ thể.
Tóm tắt lý thuyết
Ta có thể giá trị \(\beta \) là xác suất sai lầm loại 2.
Trở lại thí dụ về trọng lượng của gà khi xuất chuồng đã nêu ở phần trên. Xét cặp giả thiết.
\({H_0}:\mu = 3,4;{H_1}:\mu > 3,4\)
Ta thấy xác suất để thừa nhận giả thiết H0 sai sẽ phụ thuộc vào việc giá trị thực của \(\mu\) sai lệch nhiều hay ít so với 3,4. Chẳng hạn nếu giá trị thực của \(\mu\)
là 3,6 thì \(\beta\) sẽ nhỏ hơn trường hợp giá trị thực của \(\mu\) là 3,45. Vậy tùy thuộc vào giá trị thực của \(\mu\) mà ta có các giá trị \(\beta\) khác nhau. Điều này được minh họa trên hình 8.9-a, 8.9-b, 8.9-c tương ứng với 3 giá trị thực của \(\mu\) là : 3,48 ; 3,54 và 3,6
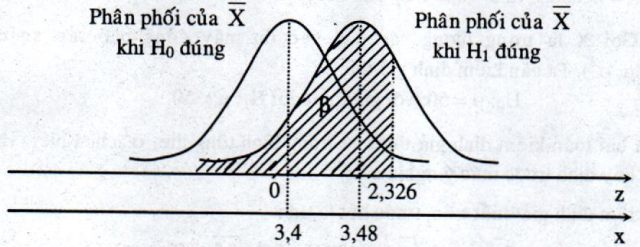
Hình 8.9-a: Trường hợp \({H_1}:\mu = 3,48\)
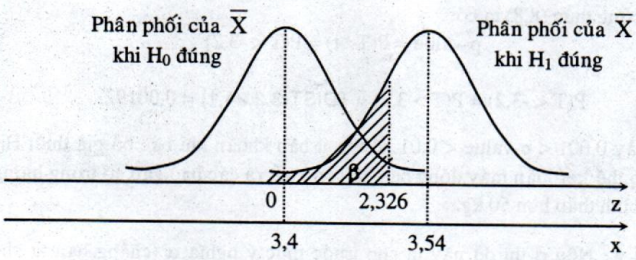
Hình 8.9-b: Trường hợp \({H_1}:\mu = 3,54\)

Hình 8.9-c: Trường hợp \({H_1}:\mu = 3,6\)
Giả sử ta vẫn kiểm định giả thiết \({H_0}:\mu = 3,4;{H_1}:\mu > 3,4\) với mức ý nghĩa \(\alpha= 0,01\). Diện tích phần gạch chéo trên các hình 8.9-a, 8.9-b, 8.9-b biểu thị giá trị của p ứng với các trường hợp giá trị thực của p là 3,48; 3,54 và 3,6.
\(\beta = P\left( {Z' < {z_{1 - \beta }}} \right) = P\left( {Z' < {z_\alpha }} \right) = P\left[ {\frac{{\overline X - {m_1}}}{{se(\overline X )}} < {z_\alpha }} \right]\)
\(= P\left[ {\frac{{\left( {\overline X - {m_0}} \right)}}{{se\left( {\overline X } \right)}} + \frac{{\left( {{m_0} - {m_1}} \right)}}{{se\left( {\overline X } \right)}} < {z_\alpha }} \right] = P\left[ {\frac{{\left( {\overline X - {m_0}} \right)}}{{se\left( {\overline X } \right)}} < {z_\alpha } - \frac{{\left( {{m_0} - {m_1}} \right)}}{{se\left( {\overline X } \right)}}} \right]\)
\(\Rightarrow \beta = P\left[ {Z < {z_\alpha } - \frac{{\left( {{m_0} - {m_1}} \right)}}{{se\left( {\overline X } \right)}}} \right]\) (8.10)
Bằng cách chứng minh tương tự ta được biểu thức của \(\beta\) khi miền bác bỏ là bên trái:
\( \beta = P\left[ {Z < {z_\alpha } - \frac{{\left( {{m_1} - {m_0}} \right)}}{{se\left( {\overline X } \right)}}} \right]\) (8.11)
Từ đó ta có công thức chung để tìm xác suất mắc phải sai lầm loại 2 khi miền bác bỏ là một phía (bên phải hoặc bên trái) như sau:
\(\beta = P\left[ {Z < {z_\alpha } - \frac{{\left| {{m_0} - {m_1}} \right|}}{{se\left( {\bar X} \right)}}} \right]\) (8.12)
Nếu kiểm định giả thiết hai phía thì p được xác định bằng công thức sau:
\(\beta = P\left[ {Z < {z_{\alpha/2} } - \frac{{\left| {{m_0} - {m_1}} \right|}}{{se\left( {\bar X} \right)}}} \right]\)
Thí dụ: Xét tiếp thí dụ về trọng lượng gà khi xuất chuồng. Tìm xác suất mắc sai lầm loại 2 và lực kiểm định nếu trọng lượng trung bình của gà khi xuất chuồng sau khi áp dụng phương pháp chăn nuôi mới là 3,52 kg.
Giải: Vì giả thiết đối là \({H_1}:\mu > 3,4\) nên với \(\alpha = 0,01; m_0 = 3,4; m_1= 3,52\). Theo công thức 8.12 ta có:
\(\beta = P\left[ {Z < {z_{0,01}} - \frac{{\left| {3,4 - 3,52} \right|}}{{0,32/\sqrt {50} }}} \right] = P\left( {Z < 2,326 - 2,65165} \right)\)
\(= P(Z < -0,33) = P(Z > 0,33) = 0,5 - \Phi (0,33) = 0,371\)
Lực kiểm định là: \(1- \beta = 1 - 0,371 = 0,629\)













