Vật lí 11 Kết Nối Tri Thức Bài 4: Bài tập về dao động điều hòa

Cho phương trình của một vật dao động điều hòa:

\(x = 5\cos (10\pi t + \frac{\pi }{6})(cm)\)

Xác định biên độ A, tần số f, pha ban đầu \(\varphi \), và li độ x₁ tại thời điểm t₁ = 0,05s.

Giải:

So sáng phương trình dao động của vật với phương trình dạng cơ bản \(x = A\cos (\omega t + \varphi )\):

Ta có:

• Biên độ A = 5 cm
• Tần số \(f = \frac{\omega }{{2\pi }} = \frac{{10\pi }}{{2\pi }} = 5Hz\)
• Pha ban đầu \(\varphi  = \frac{\pi }{6}(rad)\)
• Li độ lúc t₁:

\({x_1} = 5\cos (10\pi .0,05 + \frac{\pi }{6}) = 5\cos (\frac{{4\pi }}{6}) =  - 2,5cm\).

Một vật dao động điều hòa với tần số 2 Hz. Tại thời điểm ban đầu vật có li độ x = 5 cm và vận tốc v = -30 cm/s. Xác định:

a) Biên độ và pha ban đầu của dao động.

b) Giá trị cực đại của vận tốc và gia tốc của vật khi dao động.

Giải:

a) Tần số góc của dao động: \(\omega  = 2\pi f = 4\pi (rad/s).\)

Khi \(t = 0\left\{ {\begin{array}{*{20}{c}}
{{x_0} = A\cos \varphi  = 5cm}\\
{{v_0} =  - \omega A\sin \varphi  =  - 30cm/s}
\end{array}} \right.\)

Biên độ và pha ban đầu của dao động:

\(A = \sqrt {{x^2} + \frac{{{v^2}}}{{{\omega ^2}}}}  = \sqrt {{5^2} + \frac{{{{( - 30)}^2}}}{{{{(4\pi )}^2}}}}  \approx 5,54cm\)

\(\tan \varphi  = \frac{{\omega {x_0}}}{{{v_0}}} = \frac{{30}}{{4\pi .5}} = \frac{3}{{2\pi }} \Rightarrow \varphi  \approx 0,44rad\)

b) Vận tốc cực đại của vật: \({v_{\max }} = \omega A = 4\pi .5,54 \approx 70cm/s.\)

Gia tốc cực đại của vật: \({a_{\max }} = {\omega ^2}A = {(4\pi )^2}.5,{54.10^{ - 2}} \approx 8,8m/{s^2}.\)

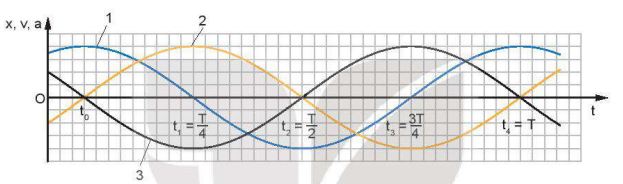
Một vật dao động điều hòa với tần số góc \(\omega  = 1\) rad/s, có đồ thị của li độ x, vận tốc v và gia tốc a theo thời gian t được mô tả trên Hình 4.1.

Hình 4.1

Hãy chỉ đúng đồ thị của li độ (x - t), vận tốc (v - t), gia tốc (a - t) theo thời gian t trên Hình 4.1.

Giải:

Ta đã biết:

- Vận tốc v sớm pha \(\frac{\pi }{2}\) so với li độ và trễ pha \(\frac{\pi }{2}\) so với gia tốc.

- Gia tốc a ngược pha so với li độ và sớm pha \(\frac{\pi }{2}\) so với vận tốc.

Do đó, trên Hình 4.1 đường 2 là đồ thị li độ x(t), đường 1 là đồ thị vận tốc v(t), đường 3 là đồ thị gia tốc a(t).

Bài tập 1: Cho một dao động điều hòa với tần số f = 2 Hz. Tại thời điểm t vật có li độ là x = 5 cm và đang chuyển động với tốc độ 20\(\pi \) cm/s theo chiều âm. Chọn gốc thời gian lúc vật đi qua vị trí  \(x =  - 2,5\sqrt 2 cm\) theo chiều dương. Viết phương trình dao động của vật

Hướng dẫn giải:

\(\omega  = 2\pi f = 4\pi (rad/s)\)

Tại thời điểm t vật ở vị trí x:

Xét tại thời điểm gốc thời gian:

\(\left\{ {\begin{array}{*{20}{c}}
{x = A\cos \varphi }\\
{v =  - \omega A\sin \varphi }
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}
{ - 2,5\sqrt 2  = 5\sqrt 2 \cos \varphi }\\
{v =  - \omega A\sin \varphi  > 0}
\end{array}} \right.} \right. \Rightarrow \varphi  =  - \frac{{2\pi }}{3}\)

Vậy phương trình dao động của vật là \(x = 5\sqrt 2 \cos (4\pi t - \frac{{2\pi }}{3})(cm)\)(cm)

Bài tập 2: Gọi v_max và a_max lần lượt là tốc độ cực đại và độ lớn gia tốc cực đại của vật dao động điều hòa. Chu kỳ T của dao động là

A. \(\frac{{{v_{\max }}}}{{{a_{\max }}}}\)

B. \(\frac{{{a_{\max }}}}{{{v_{\max }}}}\)

C. \(\frac{{{a_{\max }}}}{{2\pi {v_{\max }}}}\)

D. \(\frac{{2\pi {v_{\max }}}}{{{a_{\max }}}}\)

Hướng dẫn giải:

Ta có: \(\left\{ {\begin{array}{*{20}{c}}
{{v_{\max }} = \omega A}\\
{{a_{\max }} = {\omega ^2}A}
\end{array}} \right. \Rightarrow \frac{{{a_{\max }}}}{{{v_{\max }}}} = \omega \)

Mặt khác ta có biểu thức chu kì: \(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{\frac{{{a_{\max }}}}{{{v_{\max }}}}}} = \frac{{2\pi {v_{\max }}}}{{{a_{\max }}}}\)

Đáp án D

Học xong bài này các em cần biết: Xác định các đại lượng đặc trưng của dao động điều hòa khi biết phương trình hoặc đồ thị của vật dao động điều hòa và ngược lại.

Các em có thể hệ thống lại nội dung kiến thức đã học được thông qua bài kiểm tra Trắc nghiệm Vật lí 11 Kết Nối Tri Thức Bài 4 cực hay có đáp án và lời giải chi tiết. 

• Câu 1:

  Biểu thức li độ của vật dao động điều hòa có dạng x = Acos(2ωt + φ), vận tốc của vật có giá trị cực đại là:

  • A. v_max = A²ω 
  • B. v_max = 2Aω 
  • C. v_max = Aω ²
  • D. v_max = Aω 

• Câu 2:

  Một chất điểm dao động điều hòa với chu kỳ 0,5π s và biên độ 2 cm. Vận tốc của chất điểm tại vị trí cân bằng có độ lớn bằng

  • A. 3 cm/s
  • B. 0,5 cm/s
  • C. 4 cm/s
  • D. 8 cm/s

• Câu 3:

  Biểu thức li độ của vật dao động điều hòa có dạng: \(x =  - 8\cos 2(2\pi t + \frac{\pi }{6})\) 

  Biên độ dao động A và pha ban đầu φ của vật lần lượt là

  • A. A = 8 cm; φ = \( - \frac{{2\pi }}{3}\)
  • B. A = 8 cm; φ = \(\frac{{2\pi }}{3}\)
  • C. A = - 8 cm; φ = \(\frac{\pi }{3}\)
  • D. A = 8 cm; φ = \(\frac{\pi }{3}\)

Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức về bài học này nhé!

Các em có thể xem thêm phần hướng dẫn Giải bài tập Vật lí 11 Kết Nối Tri Thức Bài 4 để giúp các em nắm vững bài học và các phương pháp giải bài tập.

Khởi động trang 17 SGK Vật lí 11 Kết nối tri thức – KNTT

Giải Câu hỏi trang 17 SGK Vật lí 11 Kết nối tri thức – KNTT

Giải Bài tập 1 trang 18 SGK Vật lí 11 Kết nối tri thức – KNTT

Giải Bài tập 2 trang 18 SGK Vật lí 11 Kết nối tri thức – KNTT

Giải Bài tập 3 trang 19 SGK Vật lí 11 Kết nối tri thức – KNTT

Giải Bài tập 4 trang 19 SGK Vật lí 11 Kết nối tri thức – KNTT

Giải Bài tập 5 trang 19 SGK Vật lí 11 Kết nối tri thức – KNTT

Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Vật lý HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!

Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!