Giải bài 3 trang 20 SGK Toán 6 Chân trời sáng tạo tập 2 - CTST
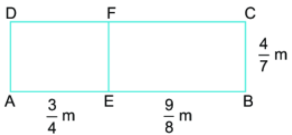
Tính diện tích hình chữ nhật ABCD ở hình bên theo hai cách, trong đó có cách tính tổng diện tích các hình chữ nhật AEFD và EBCF. Hai cách đó minh hoạ tính chất nào của phép nhân A E phân số?
Hướng dẫn giải chi tiết
Hướng dẫn giải
- Cách 1: Tính chiều rộng của hình chữ nhật ABCD sau đó tính diện tích
- Cách 2: Diện tích hình chữ nhật ABCD bằng tổng diện tích hai hình chữ nhật ADFE và BCFE.
Lời giải chi tiết
.jpg)
Cách 1:
Chiều dài hình chữ nhật ABCD là:
\(\frac{3}{4} + \frac{9}{8} = \frac{{15}}{8}\,(m)\)
Diện tích hình chữ nhật ABCD là:
\(\frac{4}{7}.\frac{{15}}{8} = \frac{{15}}{{14}}\) (m2)
=> Tính chất phân phối của phép nhân.
Cách 2:
Diện tích hình chữ nhật ADFE là:
\(\frac{3}{4}.\frac{4}{7} = \frac{3}{7}\)(m2)
Diện tích hình chữ nhật BCFE là:
\(\frac{4}{7}.\frac{9}{8} = \frac{9}{{14}}\) (m2)
Diện tích hình chữ nhật ABCD là:
\(\frac{3}{7} + \frac{9}{{14}} = \frac{{15}}{{14}}\) (m2)
=> Tính chất kết hợp của phép nhân.
-- Mod Toán 6 HỌC247
Bài tập SGK khác
Giải bài 1 trang 20 SGK Toán 6 Chân trời sáng tạo tập 2 - CTST
Giải bài 2 trang 20 SGK Toán 6 Chân trời sáng tạo tập 2 - CTST
Giải bài 1 trang 25 SBT Toán 6 Chân trời sáng tạo tập 2 - CTST
Giải bài 2 trang 25 SBT Toán 6 Chân trời sáng tạo tập 2 - CTST
Giải bài 3 trang 25 SBT Toán 6 Chân trời sáng tạo tập 2 - CTST
Giải bài 4 trang 25 SBT Toán 6 Chân trời sáng tạo tập 2 - CTST
Giải bài 5 trang 26 SBT Toán 6 Chân trời sáng tạo tập 2 - CTST
-


Người ta ước tính rằng tổng lượng nước trên Trái Đất là khoảng 1 380 triệu \(km^3\), trong đó khoảng \(\frac{{97}}{{100}}\) lượng nước là nước mặn (không uống được) và \(\frac{3}{{100}}\) lượng nước là nước ngọt.
bởi Lê Nhật Minh
 18/02/2022
18/02/2022
Trong \(\frac{3}{{100}}\)lượng nước ngọt thì có khoảng \(\frac{2}{3}\) lượng nước này tồn tại ở dạng sông băng và các mũ băng ở các cực, \(\frac{1}{3}\) lượng nước này tồn tại ở dạng nước ngầm và bề mặt Trái Đất. Hãy ước tính lượng nước ngầm và bề mặt Trái Đất.
Theo dõi (0) 1 Trả lời -


Tính giá trị của biểu thức sau đây: \({B = \frac{{ - 5}}{7}.\frac{6}{{13}}.\frac{{ - 7}}{5}.( - 39)}\)
bởi minh thuận
 19/02/2022
19/02/2022
Tính giá trị của biểu thức sau đây: \({B = \frac{{ - 5}}{7}.\frac{6}{{13}}.\frac{{ - 7}}{5}.( - 39)}\)
Theo dõi (0) 1 Trả lời -


Tính giá trị của biểu thức sau đây: \({A = \frac{{ - 9}}{{10}}.\frac{7}{{11}}.\frac{{10}}{9}.( - 22)}\)
bởi Nguyễn Trọng Nhân
 18/02/2022
18/02/2022
Tính giá trị của biểu thức sau đây: \({A = \frac{{ - 9}}{{10}}.\frac{7}{{11}}.\frac{{10}}{9}.( - 22)}\)
Theo dõi (0) 1 Trả lời -


Tính giá trị của biểu thức cho sau: \(\displaystyle {{A}} = {\displaystyle {{2 \over 3} + {2 \over 5} - {2 \over 9}} \over {\displaystyle {4 \over 3} + {4 \over 5} - {4 \over 9}}} \)
bởi Mai Hoa
 24/01/2022
24/01/2022
Tính giá trị của biểu thức cho sau: \(\displaystyle {{A}} = {\displaystyle {{2 \over 3} + {2 \over 5} - {2 \over 9}} \over {\displaystyle {4 \over 3} + {4 \over 5} - {4 \over 9}}} \)
Theo dõi (0) 1 Trả lời -
ADMICRO


Hãy viết phân số sau \(\displaystyle {{14} \over {15}}\) dưới dạng thương của hai phân số có tử và mẫu là các số nguyên dương có một chữ số.
bởi Nguyễn Thanh Trà
 24/01/2022
24/01/2022
Hãy viết phân số sau \(\displaystyle {{14} \over {15}}\) dưới dạng thương của hai phân số có tử và mẫu là các số nguyên dương có một chữ số.
Theo dõi (0) 1 Trả lời -


Một ô tô đi quãng đường \(AB\) với vận tốc \(40km/ h.\) Lúc về, xe đi quãng đường \(BA\) với vận tốc \(50km/ h.\) Thời gian cả đi lẫn về (không kể nghỉ) là \(4\) giờ \(30\) phút. Cho biết Thời gian ô tô đi \(1 km\) lúc đi ? Lúc về ?
bởi Lê Bảo An
 24/01/2022
24/01/2022
Một ô tô đi quãng đường \(AB\) với vận tốc \(40km/ h.\) Lúc về, xe đi quãng đường \(BA\) với vận tốc \(50km/ h.\) Thời gian cả đi lẫn về (không kể nghỉ) là \(4\) giờ \(30\) phút. Cho biết Thời gian ô tô đi \(1 km\) lúc đi ? Lúc về ?
Theo dõi (0) 1 Trả lời





