Hoạt động khám phá 2 trang 20 SGK Toán 11 Chân trời sáng tạo tập 2

a) Xét hàm số mũ \(y = {2^x}\) với tập xác định \(\mathbb{R}\).

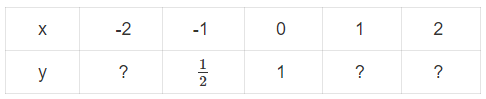
i) Hoàn thành bảng giá trị sau:

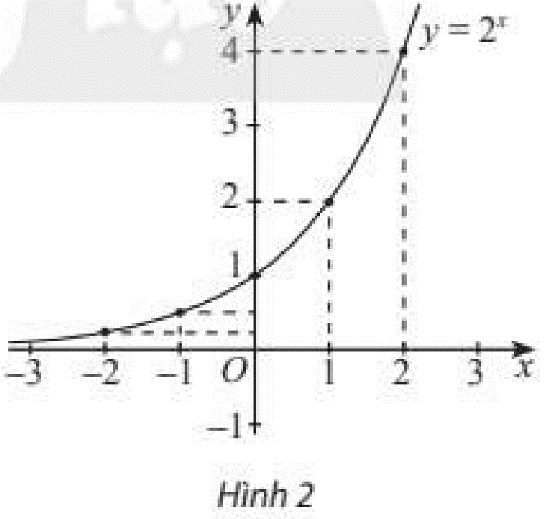
ii) Trong mặt phẳng toạ độ \(Oxy\), xác định các điểm có toạ độ như bảng trên. Làm tương tự, lấy nhiều điểm \(M\left( {x;{2^x}} \right)\) với \(x \in \mathbb{R}\) và nối lại ta được đồ thị hàm số \(y = {2^x}\) như Hình 2. Từ đồ thị nảy, nêu nhận xét về tính liên tục, tính đồng biến, nghịch biến, giới hạn khi \(x \to + \infty ,x \to - \infty \) và tập giá trị của hàm số đã cho.

b) Lập bảng giá trị và vẽ đồ thị của hàm số \(y = {\left( {\frac{1}{2}} \right)^x}\). Từ đó, nêu nhận xét về tính liên tục, tính đồng biến, nghịch biến, giới hạn khi \(x \to + \infty ,x \to - \infty \) và tập giá trị của hàm số này.

QUẢNG CÁO

Hướng dẫn giải chi tiết Hoạt động khám phá 2

Phương pháp giải:

a) Thay các giá trị của \(x\) vào hàm số sau đó dựa vào đồ thị nhận xét.

b) Lập bảng giá trị, vẽ đồ thị hàm số, sau đó dựa vào đồ thị nhận xét.

Lời giải chi tiết:

a) i)

ii) ‒ Hàm số liên tục trên \(\mathbb{R}\).

‒ Hàm số đồng biến trên \(\mathbb{R}\).

‒ Giới hạn: \(\mathop {\lim }\limits_{x \to + \infty } {2^x} = + \infty ;\mathop {\lim }\limits_{x \to - \infty } {2^x} = 0\).

‒ Tập giá trị: \(\left( {0; + \infty } \right)\).

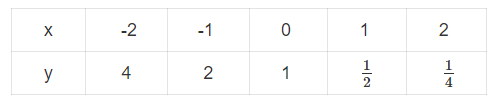
b) Bảng giá trị:

Đồ thị hàm số \(y = {\left( {\frac{1}{2}} \right)^x}\):

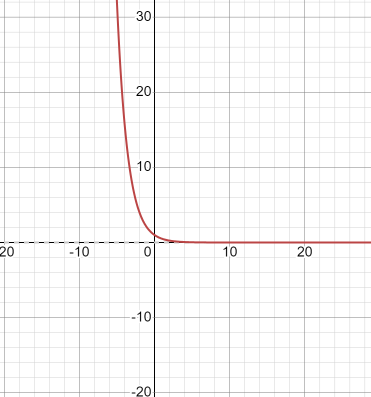
‒ Hàm số liên tục trên \(\mathbb{R}\).

‒ Hàm số nghịch biến trên \(\mathbb{R}\).

‒ Giới hạn: \(\mathop {\lim }\limits_{x \to + \infty } {\left( {\frac{1}{2}} \right)^x} = 0;\mathop {\lim }\limits_{x \to - \infty } {\left( {\frac{1}{2}} \right)^x} = + \infty \).

‒ Tập giá trị: \(\left( {0; + \infty } \right)\).

-- Mod Toán 11 HỌC247

Nếu bạn thấy hướng dẫn giải Hoạt động khám phá 2 trang 20 SGK Toán 11 Chân trời sáng tạo tập 2 - CTST HAY thì click chia sẻ