Giải Bài 5 trang 70 SGK Toán 11 Chân trời sáng tạo tập 1
Xét quá trình tạo ra hình có chu vi vô cực và diện tích bằng 0 như sau:
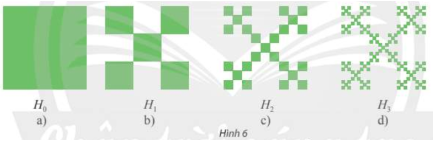
Bắt đầu bằng một hình vuông \({H_0}\) cạnh bằng 1 đơn vị độ dài (xem Hình 6a). Chia hình vuông \({H_0}\) thành chính hình vuông bằng nhau, bỏ đi bốn hình vuông, nhận được hình \({H_1}\) (xem Hình 6b). Tiếp theo, chia mỗi hình vuông của \({H_1}\) thành chín hình vuông, rồi bỏ đi bốn hình vuông, nhận được hình \({H_2}\) (xem Hình 6c). Tiếp tục quá trình này, ta nhận được một dãy hình \({H_n}\left( {n = 1,2,3,...} \right)\).
Ta có: \({H_1}\) có 5 hình vuông, mỗi hình vuông có cạnh bằng \(\frac{1}{3}\);
\({H_2}\) có \(5.5 = {5^2}\) hình vuông, mỗi hình vuông có cạnh bằng \(\frac{1}{3}.\frac{1}{3} = \frac{1}{{{3^2}}}\);…
Từ đó, nhận được hình \({H_n}\) có \({5^n}\) hình vuông, mỗi hình vuông có cạnh bằng \(\frac{1}{{{3^n}}}\).
a) Tính diện tích \({S_n}\) của \({H_n}\) và tính \(\lim {S_n}\).
b) Tính chu vi \({p_n}\) của \({H_n}\) và tính \(\lim {p_n}\).
(Quá trình trên tạo nên một hình, gọi là một fractal, được coi là có diện tích \(\lim {S_n}\) và chu vi \(\lim {p_n}\)).
Hướng dẫn giải chi tiết Bài 5
Phương pháp giải
Áp dụng công thức tính tổng của cấp số nhân lùi vô hạn có số hạng đầu \({u_1}\) và công bội \(q\): \(S = {u_1} + {u_2} + ... + {u_n} + ... = \frac{{{u_1}}}{{1 - q}}\) và công thức tính giới hạn cơ bản: \(\lim {q^n} = 0\), với \(q\) là số thực thỏa mãn \(\left| q \right| < 1\).
Lời giải chi tiết
a) \({S_n} = {5^n}.{\left( {\frac{1}{{{3^n}}}} \right)^2} = {5^n}.\frac{1}{{{9^n}}} = {\left( {\frac{5}{9}} \right)^n},n = 1,2,3,...\)
\(\lim {S_n} = \lim {\left( {\frac{5}{9}} \right)^n} = 0\)
b) \({p_n} = {5^n}.4.\frac{1}{{{3^n}}} = 4.{\left( {\frac{5}{3}} \right)^n},n = 1,2,3,...\)
\(\lim {p_n} = \lim \left( {4.{{\left( {\frac{5}{3}} \right)}^n}} \right)\)
Vì
\(\lim \frac{1}{{4.{{\left( {\frac{5}{3}} \right)}^n}}} \\= \frac{1}{4}.\lim {\left( {\frac{3}{5}} \right)^n} = 0\) và \(4.{\left( {\frac{5}{3}} \right)^n} > 0\) với mọi \(n\)
nên \(\lim {p_n} = \lim \left( {4.{{\left( {\frac{5}{3}} \right)}^n}} \right) = + \infty \).
-- Mod Toán 11 HỌC247
Bài tập SGK khác
Giải Bài 3 trang 69 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 4 trang 70 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Bài tập 1 trang 75 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 2 trang 75 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 3 trang 75 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 4 trang 76 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 5 trang 76 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 6 trang 76 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 7 trang 76 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 8 trang 76 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 9 trang 76 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 10 trang 76 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 11 trang 76 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 12 trang 77 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 13 trang 77 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.


