Bài tập 3 trang 158 SBT Toán 11 Tập 1 Chân trời sáng tạo
Thâm niên công tác của các công nhân hai nhà máy A và B.
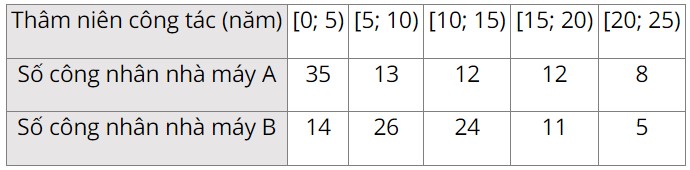
a) Hãy so sánh thâm niên công tác của nhân viên hai nhà máy theo số trung bình và trung vị.
b) Hãy ước lượng tứ phân vị thứ nhất và thứ ba của hai mẫu số liệu ghép nhóm trên.
Hướng dẫn giải chi tiết Bài tập 3
a) Bảng tần số ghép nhóm bao gồm giá trị đại diện của các nhóm như sau:
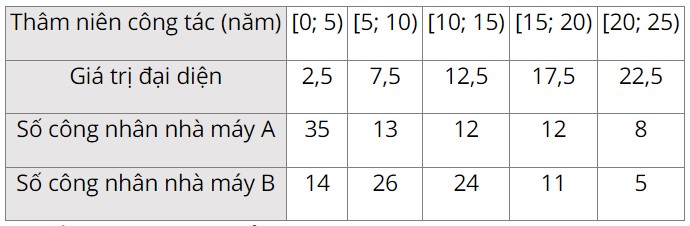
Trung bình số năm thâm niên của công nhân nhà máy A là:
= = 9,0625 (năm).
Trung bình số năm thâm niên của công nhân nhà máy B là:
= = 10,4375 (năm).
Suy ra .
Vậy nếu so sánh theo số trung bình (năm) thì thâm niên công tác của nhân viên công ty A ngắn hơn thâm niên công tác của nhân viên công ty B.
- Nhà máy A:
Gọi x1; x2; x3; ...; x80 là mẫu số liệu được xếp theo thứ tự không giảm.
Ta có:
x1, ..., x35 ∈ [0; 5); x36, ..., x48 ∈ [5; 10); x49, ..., x60 ∈ [10; 15);
x61, ..., x72 ∈ [15; 20); x73, ..., x80 ∈ [20; 25).
Cỡ mẫu nA = 80 là số chẵn nên trung vị .
Do x40 và x41 thuộc nhóm [5; 10) nên trung vị của mẫu số liệu là:
.
- Nhà máy B:
Gọi x1; x2; x3; ...; x80 là mẫu số liệu được xếp theo thứ tự không giảm.
Ta có:
x1, ..., x14 ∈ [0; 5); x15, ..., x40 ∈ [5; 10); x41, ..., x64 ∈ [10; 15);
x65, ..., x75 ∈ [15; 20); x76, ..., x80 ∈ [20; 25).
Cỡ mẫu nB = 80 là số chẵn nên trung vị .
Do x40 thuộc nhóm [5; 10) và x41 thuộc nhóm [10; 15) nên ta có Me(B) = 10.
Suy ra Me(A) < Me(B).
Vậy nếu so sánh theo trung vị thì thâm niên công tác của nhân viên công ty A ngắn hơn thâm niên công tác của nhân viên công ty B.
b) - Nhà máy A:
Tứ phân vị thứ nhất của mẫu số liệu x1; x2; x3;...; x80 là .
Do x20 và x21 thuộc nhóm [0; 5) nên tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là.
Tứ phân vị thứ ba của mẫu số liệu x1; x2; x3;...; x80 là .
Do x60 thuộc nhóm [10; 15) và x61 thuộc nhóm [15; 20) nên tứ phân vị thứ ba của mẫu số liệu ghép nhóm là Q3(A) = 15.
- Nhà máy B:
Tứ phân vị thứ nhất của mẫu số liệu x1; x2; x3;...; x80 là .
Do x20 và x21 thuộc nhóm [5; 10) nên tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
Tứ phân vị thứ ba của mẫu số liệu x1; x2; x3;...; x80 là .
Do x60 và x61 thuộc nhóm [10; 15) nên tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
-- Mod Toán 11 HỌC247
Bài tập SGK khác
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.


