Bài 3 trang 104 SGK Toán 11 Cánh diều Tập 1 - CD

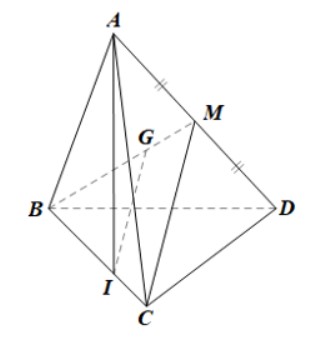
Gọi M là trung điểm của AD.

- Xét $∆$\(ABD\) có G là trọng tâm tam giác nên $\frac{BG}{GM}=\frac{2}{1}$ .

Theo bài, \(BI = 2IC\) nên $\frac{BI}{IC}=\frac{2}{1}$

- Trong mặt phẳng (\(BCM\)):

Xét $∆$\(BCM\) có: $\frac{BI}{IC}=\frac{BG}{GM}=\frac{2}{1}$ , suy ra \(IG // CM\) (định lí Thalès đảo)

- Ta có: \(IG // CM;~CM ⊂ (ACD)\)

Do đó \(IG // (ACD)\).

-- Mod Toán 11 HỌC247