Bài tập 7.30 trang 38 SBT Toán 11 Tập 2 Kết nối tri thức
Cho hình hộp chữ nhật \(ABCD \cdot A'B'C'D'\) có \(AB = a,AD = a\sqrt 2 ,AA' = a\sqrt 3 \). Tính theo a khoảng cách:
a) Từ điểm \(A\) đến mặt phẳng \(\left( {BDD'B'} \right)\).
b) Giữa hai đường thẳng \(BD\) và \(CD'\).
Hướng dẫn giải chi tiết Bài 7.30
a) Kẻ \(AH\) vuông góc với \(BD\) tại \(H\). Khi đó \(AH \bot \left( {BB'D'D} \right)\).
Suy ra \(d\left( {A,\left( {BB'D'D} \right)} \right) = AH = \frac{{AB \cdot AD}}{{BD}} = \frac{{a\sqrt 6 }}{3}\).
b) Ta có: \(CD'//\left( {A'BD} \right)\) nên\(d\left( {CD',BD} \right) = d\left( {CD',\left( {A'BD} \right)} \right) = d\left( {C,\left( {A'BD} \right)} \right){\rm{.\;}}\)
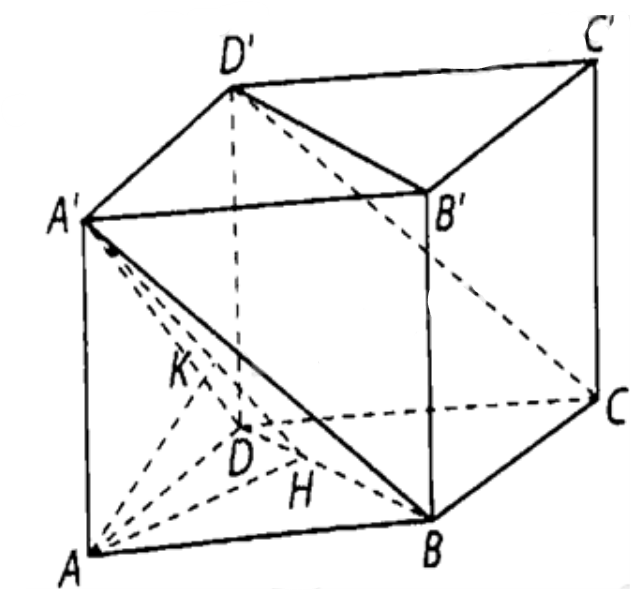
Vì \(AC\) cắt \(BD\) tại trung điểm của \(AC\) nên \(d\left( {C,\left( {A'BD} \right)} \right) = d\left( {A,\left( {A'BD} \right)} \right)\).
Kẻ \(AK\) vuông góc với \(A'H\) tại \(K\).
Khi đó \(AK \bot \left( {A'BD} \right)\).
Suy ra \(d\left( {A,\left( {A'BD} \right)} \right) = AK = \frac{{AH \cdot AA'}}{{A'H}} = \frac{{a\sqrt {66} }}{{11}}\).
Vậy \(d\left( {CD',BD} \right) = \frac{{a\sqrt {66} }}{{11}}\).
-- Mod Toán 11 HỌC247
Bài tập SGK khác
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





