Bài tập 7.20 trang 34 SBT Toán 11 Tập 2 Kết nối tri thức
Cho tứ diện \(ABCD\) có \(AC = BC,AD = BD\). Gọi \(M\) là trung điểm của \(AB\). Chứng minh rằng \(\left( {CDM} \right) \bot \left( {ABC} \right)\) và \(\left( {CDM} \right) \bot \left( {ABD} \right)\)?
Hướng dẫn giải chi tiết Bài 7.20
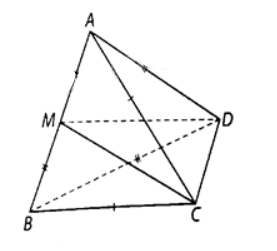
Vì \(M\) là trung điểm của \(AB\) nên \(AB \bot CM\), \(AB \bot DM\), suy ra \(AB \bot \left( {CDM} \right)\).
Vì hai mặt phẳng \(\left( {ABC} \right)\) và \(\left( {ABD} \right)\) đều chứa đường thẳng \(AB\) nên \(\left( {ABC} \right) \bot \left( {CDM} \right),\left( {ABD} \right) \bot \left( {CDM} \right)\).
-- Mod Toán 11 HỌC247
Bài tập SGK khác
Giải Bài 7.21 trang 53 SGK Toán 11 Kết nối tri thức tập 2 - KNTT
Bài tập 7.19 trang 34 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Bài tập 7.21 trang 34 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Bài tập 7.22 trang 34 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Bài tập 7.23 trang 34 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Bài tập 7.24 trang 34 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Bài tập 7.25 trang 35 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Bài tập 7.26 trang 35 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.


