-
Câu hỏi:
Cho hình hộp ABCD.A′B′C′D′. Giả sử tam giác AB′C và A′DC′ đều có 3 góc nhọn. Góc giữa hai đường thẳng AC
và A′D là góc nào sau đây?-
A.
\(\widehat {BDB'}\)
-
B.
\(\widehat {AB'C}\)
-
C.
\(\widehat {DB'B}\)
-
D.
\(\widehat {DA'C}\)
Lời giải tham khảo:
Đáp án đúng: D
Đáp án: D
Giải thích:
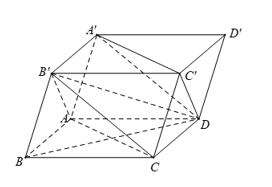
Ta có: AC // A′C′ (tính chất của hình hộp)
⇒(AC,A′D)=(A′C′,A′D) = góc DA′C′ (do giả thiết cho ΔDA′C′ nhọn).
Hãy trả lời câu hỏi trước khi xem đáp án và lời giải -
A.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
CÂU HỎI KHÁC
- Trong không gian cho ba đường thẳng phân biệt a,b,c. Tìm khẳng định đúng?
- Trong các mệnh đề dưới đây mệnh đề đúng là? Cho hai đường thẳng song song, đường thẳng nào vuông góc với đường thẳng thứ nhất thì cũng vuông góc với đường thẳng thứ hai
- Trong các mệnh đề sau, mệnh đề nào đúng? Góc giữa hai đường thẳng a và b bằng
- Cho hai đường thẳng phân biệt a,b và mặt phẳng (P)
- Cho tứ diện ABCD có AB=CD . Gọi I,J,E,F lần lượt là trung điểm của AC,BC,BD,AD.
- Trong không gian cho hai hình vuông ABCD và ABC'D' có chung cạnh AB
- Cho tứ diện ABCD có \(AB = CD = a,\,\,{\rm{IJ = }}\frac{{a\sqrt 3 }}{2}\)
- Hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì:
- Cho hình hộp ABCD.A′B′C′D′. Giả sử tam giác AB′C và A′DC′ đều có 3 góc nhọn
- Cho tứ diện ABCD có hai cặp cạnh đối vuông góc. Trong các mệnh đề sau mệnh đề nào đúng?

