-
Câu hỏi:
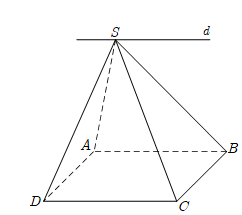
Cho hình chóp \(S.ABCD,\) đáy \(ABCD\) là hình bình hành. Giao tuyến của 2 mp \(\left( SAD \right)\) và \(\left( SBC \right)\) là đường thẳng song song với đường thẳng nào?
-
A.
\(AD.\)
-
B.
\(AC.\)
-
C.
\(DC.\)
-
D.
\(BD.\)
Lời giải tham khảo:
Đáp án đúng: A
Từ giả thiết ta có
\(\left\{ \begin{align} & \left( SAD \right)\cap \left( SBC \right)=Sx \\ & AD\ \text{//}\ BC \\ & AD\subset \left( SAD \right) \\ & BC\subset \left( SBC \right) \\ \end{align} \right.\) \(\quad \Rightarrow \ \left( SAD \right)\cap \left( SBC \right)=Sx\ \text{//}AD\ \text{//}\ BC.\)
Chọn A.
Hãy trả lời câu hỏi trước khi xem đáp án và lời giải -
A.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
QUẢNG CÁO
CÂU HỎI KHÁC
- Cho hai đường thẳng phân biệt \(a\) và \(b\) trong không gian. Có bao nhiêu vị trí tương đối giữa a & b?
- Cho hình chóp \(S.ABCD\) với đáy là tứ giác \(ABCD\) có các cạnh đối không song song. Giả sử
- Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Gọi \(d\) là giao tuyến của 2 mp \(\left( SAD \right)\And \left( SBC \right)\). Khẳng định nào sau đây đúng?
- Tìm mệnh đề đúng trong các mệnh đề bên dưới đây?
- Cho hình chóp \(S.ABCD,\) đáy \(ABCD\) là hình bình hành. Giao tuyến của 2 mp \(\left( SAD \right)\) và \(\left( SBC \right)\) là đường thẳng song song với đường thẳng nào?
- Cho 2 đường thẳng chéo nhau \(a\) và \(b\). Lấy hai điểm \(A,B\) phân biệt thuộc \(a\) và hai điểm \(C,D\) phân biệt thuộc \(b\). Khi đó 2 đường thẳng \(A\text{D}\) và \(BC\) ở vị trí gì?
- Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang, \(AB\text{//}CD\). Gọi M, N, Q lần lượt là trung
- Cho các mệnh đề sau: Số mệnh đề đúng là bao nhiêu?
- Cho hình chóp tứ giác \(S.ABCD\), \(AC\) và \(BD\) cắt nhau tại \(O\). Giao tuyến của 2 mp \(\left( SAC \right)\) và \(\left( SBD \right)\) là đường thẳng?
- Cho 2 đường thẳng chéo nhau \(a\) và \(b\). Lấy các điểm phân biệt \(A,\,B\in a;\,C,D\in b\). Khẳng định nào đúng?
VIDEO
YOMEDIA
ADMICRO
