Viб»Үc nghiГӘn cб»©u cГЎc quГЎ trГ¬nh dao Д‘б»ҷng Д‘iб»Ғu hoГ Д‘б»ғ б»©ng dб»Ҙng vГ o thб»ұc tiб»…n nhЖ° xГўy dб»ұng mГҙ hГ¬nh dб»ұ bГЎo Д‘б»ҷng Д‘бәҘt yГӘu cбә§u ta phбәЈi mГҙ tбәЈ chГӯnh xГЎc trбәЎng thГЎi của vбәӯt dao Д‘б»ҷng tбәЎi nhб»Ҝng thб»қi Д‘iб»ғm xГЎc Д‘б»Ӣnh. NgoГ i ra, dao Д‘б»ҷng Д‘iб»Ғu hoГ cГі tГӯnh chбәҘt tuбә§n hoГ n theo thб»қi gian vГ bб»Ӣ giб»ӣi hбәЎn trong khГҙng gian thГ¬ phЖ°ЖЎng trГ¬nh li Д‘б»ҷ, vбәӯn tб»‘c vГ gia tб»‘c của vбәӯt dao Д‘б»ҷng Д‘iб»Ғu hoГ cГі nhб»Ҝng khГЎc biб»Үt gГ¬ so vб»ӣi chuyб»ғn Д‘б»ҷng thбәіng Д‘б»Ғu vГ biбәҝn Д‘б»•i Д‘б»Ғu mГ em Д‘ГЈ hб»Қc б»ҹ chЖ°ЖЎng trГ¬nh Vбәӯt lГӯ 10? Дҗб»ғ Д‘i sГўu vГ o vбәҘn Д‘бә§ nГ y, chГәng ta hГЈy cГ№ng HOC247 tбәӯp trung vГ o mб»ҷt chủ Д‘б»Ғ hбәҝt sб»©c thГә vб»Ӣ vГ Д‘бә·c biб»Үt lГ "PhЖ°ЖЎng trГ¬nh dao Д‘б»ҷng Д‘iб»Ғu hГІa" thuб»ҷc ChЖ°ЖЎng 1 Vбәӯt lГӯ 11 ChГўn trб»қi sГЎng tбәЎo. Mб»қi cГЎc em cГ№ng tham khбәЈo!
TГіm tбәҜt lГҪ thuyбәҝt
1.1. Li Д‘б»ҷ trong dao Д‘б»ҷng Д‘iб»Ғu hoГ
a. PhЖ°ЖЎng trГ¬nh li Д‘б»ҷ của vбәӯt dao Д‘б»ҷng
PhЖ°ЖЎng trГ¬nh li Д‘б»ҷ của vбәӯt dao Д‘б»ҷng Д‘iб»Ғu hoГ cГі dбәЎng:
x = Acos(Пүt + ПҶ0)
Trong Д‘Гі:
+ x, A lбә§n lЖ°б»Јt lГ li Д‘б»ҷ vГ biГӘn Д‘б»ҷ dao Д‘б»ҷng của vбәӯt, trong hб»Ү SI cГі Д‘ЖЎn vб»Ӣ lГ m.
+ Пү lГ tбә§n sб»‘ gГіc của dao Д‘б»ҷng, trong hб»Ү SI cГі Д‘ЖЎn vб»Ӣ lГ rad/s.
+ ПҶ = Пүt + ПҶ0 lГ pha của dao Д‘б»ҷng, trong hб»Ү SI cГі Д‘ЖЎn vб»Ӣ lГ rad.
+ ПҶ0 lГ pha ban Д‘бә§u của dao Д‘б»ҷng, trong hб»Ү SI cГі Д‘ЖЎn vб»Ӣ lГ rad.
b. Дҗб»ҷ dб»Ӣch chuyб»ғn của vбәӯt dao Д‘б»ҷng
Li Д‘б»ҷ cЕ©ng chГӯnh lГ Д‘б»ҷ dб»Ӣch chuyб»ғn tб»« vб»Ӣ trГӯ cГўn bбәұng Д‘бәҝn vб»Ӣ trГӯ của vбәӯt tбәЎi thб»қi Д‘iб»ғm t.
\(\begin{array}{l}
d = \Delta x = x - {x_0}\\
= Acos(\omega t + {\varphi _0}) - Acos{\varphi _0}
\end{array}\)
1.2. Vбәӯn tб»‘c trong dao Д‘б»ҷng Д‘iб»Ғu hoГ
PhЖ°ЖЎng trГ¬nh vбәӯn tб»‘c của vбәӯt dao Д‘б»ҷng Д‘iб»Ғu hГІa cГі dбәЎng:
\(\begin{array}{l}
v = \omega A\cos (\omega t + {\varphi _0} + \frac{\pi }{2})\\
= - \omega A\sin (\omega t + {\varphi _0})
\end{array}\)
1.3. Gia tб»‘c trong dao Д‘б»ҷng Д‘iб»Ғu hГІa
a. PhЖ°ЖЎng trГ¬nh gia tб»‘c của vбәӯt dao Д‘б»ҷng
PhЖ°ЖЎng trГ¬nh gia tб»‘c của vбәӯt dao Д‘б»ҷng Д‘iб»Ғu hГІa cГі dбәЎng:
\(\begin{array}{l}
a = {\omega ^2}A\cos (\omega t + {\varphi _0} + \pi )\\
= - {\omega ^2}A\cos (\omega t + {\varphi _0}) = - {\omega ^2}x
\end{array}\)
b. Vбәӯn dб»Ҙng phЖ°ЖЎng trГ¬nh gia tб»‘c, mб»‘i liГӘn hб»Ү giб»Ҝa gia tб»‘c vГ li Д‘б»ҷ của vбәӯt dao Д‘б»ҷng
VГӯ dб»Ҙ: Mб»ҷt vбәӯt dao Д‘б»ҷng Д‘iб»Ғu hoГ cГі phЖ°ЖЎng trГ¬nh gia tб»‘c
\(a = 12{\pi ^2}cos{\rm{(}}2\pi t + \frac{\pi }{2}{\rm{)}}\left( {cm/s} \right)\)
a) XГЎc Д‘б»Ӣnh biГӘn Д‘б»ҷ, tбә§n sб»‘ gГіc, chu kГ¬, tбә§n sб»‘ dao Д‘б»ҷng của vбәӯt.
b) Viбәҝt phЖ°ЖЎng trГ¬nh li Д‘б»ҷ vГ phЖ°ЖЎng trГ¬nh vбәӯn tб»‘c của vбәӯt.
HЖ°б»ӣng dбә«n giбәЈi
a) Tб»« cГҙng thб»©c trГӘn, ta cГі:
\(\begin{array}{l}
a = {\omega ^2}A\cos (\omega t + {\varphi _0} + \pi )\\
= - {\omega ^2}A\cos (\omega t + {\varphi _0}) = - {\omega ^2}x
\end{array}\)
So sГЎnh vб»ӣi phЖ°ЖЎng trГ¬nh gia tб»‘c của vбәӯt, suy ra:
вҖ“ Tбә§n sб»‘ gГіc: \(\omega = 2\pi rad/s\).
вҖ“ BiГӘn Д‘б»ҷ dao Д‘б»ҷng: \(\begin{array}{l}
A = \frac{{{a_{\max }}}}{{{\omega ^2}}}\\
= \frac{{12{\pi ^2}}}{{{{(2\pi )}^2}}} = 3cm
\end{array}\).
вҖ“ Pha ban Д‘бә§u của dao Д‘б»ҷng: \({\varphi _0} = \frac{\pi }{2} - \pi = - \frac{\pi }{2}\) rad.
вҖ“ Chu kГ¬ dao Д‘б»ҷng: \(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{2\pi }} = 1s\).
вҖ“ Tбә§n sб»‘ dao Д‘б»ҷng: f = 1/T = 1/1 = 1 Hz.
b)
- PhЖ°ЖЎng trГ¬nh li Д‘б»ҷ của vбәӯt:
\(x = A\cos (\omega t + {\varphi _0}) = 3\cos (2\pi t - \frac{\pi }{2})(cm)\)
- PhЖ°ЖЎng trГ¬nh vбәӯn tб»‘c của vбәӯt:
\(v = \omega A\cos (\omega t + {\varphi _0} + \frac{\pi }{2}) = 6\pi \cos (2\pi t)(cm/s)\)
BГ i tбәӯp minh hб»Қa
BГ i tбәӯp 1: Mб»ҷt vбәӯt dao Д‘б»ҷng Д‘iб»Ғu hГІa vб»ӣi phЖ°ЖЎng trГ¬nh x = 4cos(2ПҖt + ПҖ/2) cm. XaМҒc Д‘iМЈnh biГӘn Д‘ГҙМЈ, chu kyМҖ vaМҖ viМЈ triМҒ ban Д‘ГўМҖu cuМүa vГўМЈt?
HЖ°б»ӣng dбә«n giбәЈi
ДҗГҙМҖng nhГўМҒt phЖ°ЖЎng triМҖnh vЖЎМҒi phЖ°ЖЎng triМҖnh chuГўМүn dao Д‘ГҙМЈng Д‘iГӘМҖu hoМҖa x = Acos(Пүt + ПҶ), ta Д‘Ж°ЖЎМЈc:
A = 4; Пү = 2ПҖ
вҶ’ \(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{2\pi }} = 1s;\)
ThЖЎМҖi Д‘iГӘМүm ban Д‘ГўМҖu laМҖ luМҒc t = 0, thay vaМҖo phЖ°ЖЎng triМҖnh, Д‘Ж°ЖЎМЈc x = 4cos (ПҖ/2) = 0, thЖЎМҖi Д‘iГӘМүm ban Д‘ГўМҖu vГўМЈt Д‘ang ЖЎМү viМЈ triМҒ cГўn bДғМҖng.
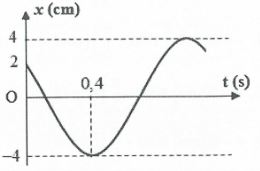
BГ i tбәӯp 2: Дҗб»“ thб»Ӣ dao Д‘б»ҷng Д‘iб»Ғu hГІa của mб»ҷt vбәӯt nhЖ° hГ¬nh vбәҪ. Viбәҝt phЖ°ЖЎng trГ¬nh dao Д‘б»ҷng của vбәӯt.
HЖ°б»ӣng dбә«n giбәЈi
Tб»« Д‘б»“ thб»Ӣ ta thбәҘy rбәұng:
\(\begin{array}{l}
\;\left\{ {\begin{array}{*{20}{c}}
{{x_0} = \frac{A}{2} = 2\;(cm)}\\
{{v_0} < 0}
\end{array}} \right.\\
\Rightarrow {\varphi _0} = \frac{\pi }{3}
\end{array}\)
LбәЎi cГі:
\(\begin{array}{l}
{t_{\left( {2 \to 0 \to - 4} \right)}} = {t_{\left( {\frac{A}{2} \to 0 \to - A} \right)}} = 0,4s\\
\Rightarrow \frac{T}{{12}} + \frac{T}{4} = 0,4\\
\Rightarrow T = 1,2s
\end{array}\)
\( \Rightarrow \omega = \frac{{2\pi }}{T} = \frac{{5\pi }}{3}\)
Vбәӯy phЖ°ЖЎng trГ¬nh dao Д‘б»ҷng của vбәӯt lГ :
\(x = 4\cos \left( {\frac{{5\pi t}}{3} + \frac{\pi }{3}} \right){\rm{\;(cm)}}\)
Luyб»Үn tбәӯp BГ i 2 Vбәӯt lГҪ 11 ChГўn trб»қi sГЎng tбәЎo
Hб»Қc xong bГ i nГ y cГЎc em cбә§n biбәҝt:
вҖ“ Дҗб»ҷ dб»Ӣch chuyб»ғn, vбәӯn tб»‘c vГ gia tб»‘c trong dao Д‘б»ҷng Д‘iб»Ғu hoГ .
вҖ“ CГЎc phЖ°ЖЎng trГ¬nh vб»Ғ li Д‘б»ҷ, vбәӯn tб»‘c vГ gia tб»‘c của dao Д‘б»ҷng Д‘iб»Ғu hoГ .
вҖ“ Mб»‘i liГӘn hб»Ү giб»Ҝa gia tб»‘c vГ li Д‘б»ҷ trong dao Д‘б»ҷng Д‘iб»Ғu hoГ .
3.1. TrбәҜc nghiб»Үm BГ i 2 Vбәӯt lГҪ 11 ChГўn trб»қi sГЎng tбәЎo
CГЎc em cГі thб»ғ hб»Ү thб»‘ng lбәЎi nб»ҷi dung kiбәҝn thб»©c Д‘ГЈ hб»Қc Д‘Ж°б»Јc thГҙng qua bГ i kiб»ғm tra TrбәҜc nghiб»Үm Vбәӯt lГӯ 11 ChГўn Trб»қi SГЎng TбәЎo BГ i 2 cб»ұc hay cГі Д‘ГЎp ГЎn vГ lб»қi giбәЈi chi tiбәҝt.
-
- A. \(x = Acot(\omega t+\varphi_{o})\)
- B. \(x = Asin(\omega t + \varphi_{o})\)
- C. \(x = Acos(\omega t + \varphi_{o})\)
- D. \(x = Acos(\omega + \varphi_{o})\)
-
- A. BiГӘn Д‘б»ҷ A
- B. Tбә§n sб»‘ gГіc Пү
- C. Pha dao Д‘б»ҷng (Пүt+ПҶ0)
- D. Chu kб»і dao Д‘б»ҷng T
-
- A. v = Acos(Пүt+ПҶ0)
- B. v = AПүcos(Пүt+ПҶ0)
- C. v = вҲ’Asin(Пүt+ПҶ0)
- D. v = вҲ’AПүsin(Пүt+ПҶ0)
CГўu 4-10: Mб»қi cГЎc em Д‘Дғng nhбәӯp xem tiбәҝp nб»ҷi dung vГ thi thб»ӯ Online Д‘б»ғ củng cб»‘ kiбәҝn thб»©c vб»Ғ bГ i hб»Қc nГ y nhГ©!
3.2. BГ i tбәӯp SGK BГ i 2 Vбәӯt lГҪ 11 ChГўn trб»қi sГЎng tбәЎo
CГЎc em cГі thб»ғ xem thГӘm phбә§n hЖ°б»ӣng dбә«n GiбәЈi bГ i tбәӯp Vбәӯt lГӯ 11 ChГўn Trб»қi SГЎng TбәЎo BГ i 2 Д‘б»ғ giГәp cГЎc em nбәҜm vб»Ҝng bГ i hб»Қc vГ cГЎc phЖ°ЖЎng phГЎp giбәЈi bГ i tбәӯp.
Khб»ҹi Д‘б»ҷng trang 14 SGK Vбәӯt lГӯ 11 ChГўn trб»қi sГЎng tбәЎo вҖ“ CTST
GiбәЈi CГўu hб»Ҹi 1 trang 14 SGK Vбәӯt lГӯ 11 ChГўn trб»қi sГЎng tбәЎo вҖ“ CTST
Luyб»Үn tбәӯp trang 15 SGK Vбәӯt lГӯ 11 ChГўn trб»қi sГЎng tбәЎo вҖ“ CTST
GiбәЈi CГўu hб»Ҹi 2 trang 15 SGK Vбәӯt lГӯ 11 ChГўn trб»қi sГЎng tбәЎo вҖ“ CTST
Luyб»Үn tбәӯp trang 16 SGK Vбәӯt lГӯ 11 ChГўn trб»қi sГЎng tбәЎo вҖ“ CTST
GiбәЈi CГўu hб»Ҹi 3 trang 17 SGK Vбәӯt lГӯ 11 ChГўn trб»қi sГЎng tбәЎo вҖ“ CTST
GiбәЈi CГўu hб»Ҹi 4 trang 17 SGK Vбәӯt lГӯ 11 ChГўn trб»қi sГЎng tбәЎo вҖ“ CTST
Luyб»Үn tбәӯp trang 18 SGK Vбәӯt lГӯ 11 ChГўn trб»қi sГЎng tбәЎo вҖ“ CTST
GiбәЈi CГўu hб»Ҹi 5 trang 19 SGK Vбәӯt lГӯ 11 ChГўn trб»қi sГЎng tбәЎo вҖ“ CTST
Luyб»Үn tбәӯp trang 19 SGK Vбәӯt lГӯ 11 ChГўn trб»қi sГЎng tбәЎo вҖ“ CTST
Vбәӯn dб»Ҙng trang 19 SGK Vбәӯt lГӯ 11 ChГўn trб»қi sГЎng tбәЎo вҖ“ CTST
GiбәЈi BГ i tбәӯp 1 trang 21 SGK Vбәӯt lГӯ 11 ChГўn trб»қi sГЎng tбәЎo вҖ“ CTST
GiбәЈi BГ i tбәӯp 2 trang 21 SGK Vбәӯt lГӯ 11 ChГўn trб»қi sГЎng tбәЎo вҖ“ CTST
GiбәЈi BГ i tбәӯp 3 trang 21 SGK Vбәӯt lГӯ 11 ChГўn trб»қi sГЎng tбәЎo вҖ“ CTST
Hб»Ҹi Д‘ГЎp BГ i 2 Vбәӯt lГҪ 11 ChГўn trб»қi sГЎng tбәЎo
Trong quГЎ trГ¬nh hб»Қc tбәӯp nбәҝu cГі thбәҜc mбәҜc hay cбә§n trб»Ј giГәp gГ¬ thГ¬ cГЎc em hГЈy comment б»ҹ mб»Ҙc Hб»Ҹi Д‘ГЎp, Cб»ҷng Д‘б»“ng Vбәӯt lГҪ HOC247 sбәҪ hб»— trб»Ј cho cГЎc em mб»ҷt cГЎch nhanh chГіng!
ChГәc cГЎc em hб»Қc tбәӯp tб»‘t vГ luГҙn Д‘бәЎt thГ nh tГӯch cao trong hб»Қc tбәӯp!
-- Mod Vбәӯt LГҪ 11 Hб»ҢC247