Trong bài học trước, chúng ta đã tìm hiểu dao động điều hoà và định nghĩa các đại lượng mô tả dao động điều hoà. Trong Bài 2: Một số dao động điều hòa thường gặp trong chương trình Vật lí 11 Cánh Diều này, chúng ta sẽ sử dụng các đại lượng đó để mô tả một số dao động điều hoà thường gặp trong cuộc sống. Mời các em cùng theo dõi.
Tóm tắt lý thuyết
1.1. Con lắc đơn
1.1.1. Cấu tạo của con lắc đơn
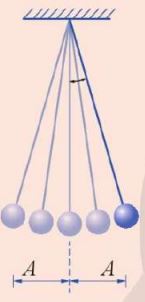
Hình 2.1. Quả cầu dao động với biên độ A
· Con lắc đơn gồm một vật nhỏ, khối lượng m, treo ở đầu một sợi dây mảnh hoặc một thanh nhẹ không giãn có chiều dài l.
· Nếu con lắc chỉ chịu tác dụng của trọng lực, khi vật ở vị trí cân bằng, dây treo có phương thẳng đứng. Khi vật được kéo lệch khỏi vị trí cân bằng một đoạn nhỏ rồi buông tay thì ta sẽ có được dao động điều hoà của con lắc đơn.
1.2. Chu kì của con lắc đơn
· Chu kì dao động của con lắc đơn không phụ thuộc vào biên độ dao động mà chỉ phụ thuộc vào chiều dài dây treo và gia tốc rơi tự do tại nơi treo con lắc.
\(T = 2\pi \sqrt {\frac{l}{g}} \)
Trong đó:
- là chiều dài dây treo, đơn vị đo là m.
- g là gia tốc rơi tự do tại nơi treo con lắc, đơn vị là m/s2.
- T là chu kì dao động của con lắc, đơn vị đo là s.
1.2. Con lắc lò xo
1.2.1. Cấu tạo con lắc lò xo
a)
b)
Hình 2.2. a) Con lắc lò xo treo thẳng đứng; b) Con lắc lò xo nằm ngang
· Con lắc lò xo là một hệ dao động gồm vật nhỏ khối lượng m gắn vào đầu một lò xo có độ cứng k, khối lượng không đáng kể, đầu kia của lò xo được giữ cố định.
· Vị trí cân bằng là vị trí hợp lực tác dụng lên vật bằng 0.
1.2.2. Chu kì của con lắc lò xo
· Chu kì dao động của con lắc lò xo không phụ thuộc vào biên độ dao động mà chỉ phụ thuộc vào đặc điểm cấu tạo của con lắc.
\(T = 2\pi \sqrt {\frac{m}{k}} \)
Trong đó:
- m là khối lượng của vật gắn với lò xo, đơn vị đo là kg.
- k là độ cứng của lò xo, đơn vị đo là N/m.
- T là chu kì dao động của con lắc, đơn vị đo là s.
1.3. Vận dụng các phương trình của dao động điều hòa
Một con lắc lò xo thẳng đứng gồm vật nặng có khối lượng 100g và một lò xo nhẹ có độ cứng k = 100N/m. Kéo vật xuống dưới theo phương thẳng đứng đến vị trí lò xo dãn 4cm rồi truyền cho nó một vận tốc 40π cm/s theo phương thẳng đứng từ dưới lên. Coi vật dao động điều hoà theo phương thẳng đứng. Thời gian ngắn nhất để vật chuyển động từ vị trí thấp nhất đến vị trí lò xo bị nén 1,5 cm là
Tần số góc của dao động
\(\omega = \sqrt {\frac{k}{m}} = \sqrt {\frac{{100}}{{0,1}}} = 10\pi \,\,{rad/s}.\)
+ Độ biến dạng của lò xo tại vị trí cân bằng \(\Delta {l_0} = \frac{{mg}}{k} = \frac{{0,1.10}}{{100}} = 1\,\,cm.\)
\( \to \) Kéo vật đến vị trí lò xo giãn 4 cm \( \to {x_0} = 3\,\,cm\), biến độ dao động của vật
\(A = \sqrt {x_0^2 + {{\left( {\frac{{{v_0}}}{\omega }} \right)}^2}} = \sqrt {{3^2} + {{\left( {\frac{{40\pi }}{{10\pi }}} \right)}^2}} = 5\,\,cm.\)
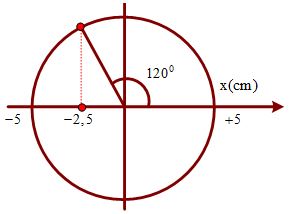
+ Vị trí lò xo bị nến 1,5 cm tương ứng với vị trí có li đô \(x = - 2,5\,\,cm\) như hình vẽ, ta có:
\(\Delta t = \frac{T}{4} + \frac{T}{{12}} = \frac{1}{{15}}\,\,s.\)
|
• Con lắc lò xo là một hệ dao động điều hoà với chu kì: \(T = 2\pi \sqrt {\frac{m}{k}} \) Trong đó - m là khối lượng của vật, có đơn vị là kg - k là độ cứng của lò xo, có đơn vị là N/m • Khi dao động với biên độ nhỏ, con lắc đơn dao động điều hoà với chu kì: \(T = 2\pi \sqrt {\frac{l}{g}} \) Trong đó - l là chiều dài dây treo, có đơn vị là m - g là gia tốc rơi tự do tại nơi treo con lắc, có đơn vị là m/s2 |
Bài tập minh họa
Ví dụ 1: Con lắc đơn (chiều dài không đổi), dao động với biên độ nhỏ có chu kỳ phụ thuộc vào
A. khối lượng của con lắc.
B. trọng lượng của con lắc.
C. tỉ số giữa khối lượng và trọng lượng của con lắc.
D. khối lượng riêng của con lắc.
Hướng dẫn giải
Con lắc đơn (chiều dài không đổi), dao động với biên độ nhỏ có chu kỳ phụ thuộc vào tỉ số giữa khối lượng và trọng lượng của con lắc.
Đáp án C
Ví dụ 2: Một đồng hồ quả lắc chạy đúng tại một nơi trên mặt đất. Người ta đưa đồng hồ từ mặt đất lên độ cao h=5km, bán kính trái đất là R=6400km (coi nhiệt độ không đổi). Mỗi ngày 1 đêm đồng hộ chạy nhanh hay chậm hơn bao nhiêu ?
Hướng dẫn giải
Chạy đúng: \(T = 2\pi \sqrt {\frac{l}{g}} \)
Chạy sai: \(T' = 2\pi \sqrt {\frac{l}{g}} \), Với gia tốc trọng trường \(g\prime = g(\frac{R}{{R + h}})2\)
Tỷ số: \(\frac{{T'}}{T} = \frac{{g'}}{g} = \frac{R}{{R + h}} < 1\) nên đồng hồ chạy nhanh.
Một ngày đêm sẽ nhanh
\({\rm{\Delta }}t = 24.60.60.\mid \frac{{T\prime }}{T} - 1\mid = 24.60.60.\frac{h}{{R + h}} = 67,45(s) \approx 68(s)\)
Luyện tập Bài 2 Vật lý 11 Cánh diều
Học xong bài này các em cần biết:
- Vận dụng được các phương trình về li độ, vận tốc và gia tốc của dao động điều hoà.
- Vận dụng được phương trình \(a = - {\omega ^2}x\) của dao động điều hoà.
3.1. Trắc nghiệm Bài 2 Vật lý 11 Cánh diều
Các em có thể hệ thống lại nội dung kiến thức đã học được thông qua bài kiểm tra Trắc nghiệm Vật lí 11 Cánh diều Bài 2 cực hay có đáp án và lời giải chi tiết.
Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức về bài học này nhé!
3.2. Bài tập SGK Bài 2 Vật lý 11 Cánh diều
Các em có thể xem thêm phần hướng dẫn Giải bài tập Vật lí 11 Cánh diều Bài 2 để giúp các em nắm vững bài học và các phương pháp giải bài tập.
Mở đầu trang 18 SGK Vật lí 11 Cánh diều - CD
Giải Câu hỏi 1 trang 19 SGK Vật lí 11 Cánh diều - CD
Luyện tập 1 trang 30 SGK Vật lí 11 Cánh diều - CD
Luyện tập 2 trang 21 SGK Vật lí 11 Cánh diều - CD
Vận dụng trang 22 SGK Vật lí 11 Cánh diều - CD
Tìm hiểu thêm trang 23 SGK Vật lí 11 Cánh diều - CD
Hỏi đáp Bài 2 Vật lý 11 Cánh diều
Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Vật lý HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!
Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!
-- Mod Vật Lý 11 HỌC247