Nội dung bài Ôn tập cuối năm Hình học 11 sẽ giúp các em hệ thống hóa lý thuyết và các dạng bài tập trong chương trình xoay quanh Phép dời hình, Phép đồng dạng, Hình học không gian. Qua đó sẽ giúp các em nắm được những vấn đề kiến thức nền tảng, trọng tâm nhất để chuẩn bị cho chương trình lớp 12 và các kì thi THPT Quốc gia
Tóm tắt lý thuyết
1. Phép dời hình và phép đồng dạng trong mặt phẳng
.png)
2. Hệ thống kiến thức hình học không gian lớp 11
- Chương trình hình học không gian lớp 11 có thể chia thành 5 bài tập lớn như sau:
a) Bài toán 1
- Tìm tương giao, bao gồm: Giao điểm của hai đường thẳng, giao điểm của đường với mặt và giao tuyến của hai mặt phẳng.
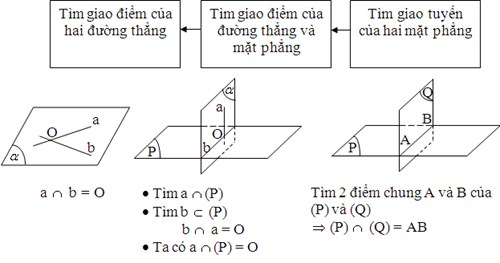
b) Bài toán 2
- Quan hệ song song, bao gồm chứng minh và dựng hình: Hai đường thẳng song song, đường thẳng song song với mặt phẳng, hai mặt phẳng song song.
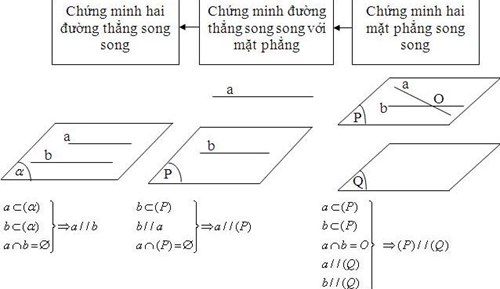
c) Bài toán 3
- Quan hệ vuông góc bao gồm chứng minh và dựng hình: Hai đường thẳng vuông góc, đường thẳng vuông góc với mặt phẳng, hai mặt phẳng vuông góc.
.jpg)
d) Bài toán 4
- Bài toán về góc bao gồm xác định và tính: Góc giữa hai đường thẳng, góc giữa đường thẳng và mặt phẳng, góc giữa hai mặt phẳng.
e) Bài toán 5
- Bài toán về khoảng cách bao gồm xác định và tính: Khoảng cách từ một điểm đến một đường thẳng, khoảng cách từ một điểm đến một mặt phẳng, khoảng cách giữa hai đường thẳng song song, khoảng cách giữa hai mặt phẳng song song, khoảng cách giữa hai đường thẳng chéo nhau.
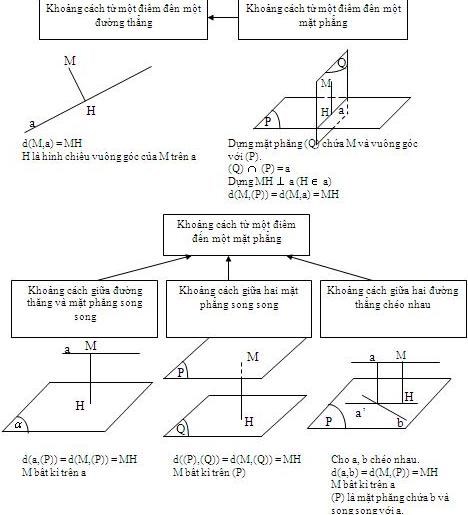
Bài tập minh họa
Ví dụ 1:
Cho hình chóp tam giác S.ABC có SA = SB =SC và có \(\widehat {{\rm{ASB}}} = \widehat {BSC} = \widehat {CSA}.\)
Chứng minh rằng: \(SA \bot BC, SB\bot AC, SC \bot AB.\)
Hướng dẫn giải:
Xét các tích vô hướng: \(\overrightarrow {SA} .\overrightarrow {BC} ,\overrightarrow {SB} .\overrightarrow {AC} ,\overrightarrow {SC} .\overrightarrow {AB} .\)
Ta có:
\(\begin{array}{l} \overrightarrow {SA} .\overrightarrow {BC} = \overrightarrow {SA} .(\overrightarrow {SC} - \overrightarrow {SB} ) = \overrightarrow {SA} .\overrightarrow {SC} - \overrightarrow {SA} .\overrightarrow {SB} \\ = \left| {\overrightarrow {SA} } \right|.\left| {\overrightarrow {SC} } \right|.c{\rm{os}}\widehat {{\rm{CSA}}} - \left| {\overrightarrow {SA} } \right|.\left| {\overrightarrow {SB} } \right|c{\rm{os}}\widehat {{\rm{ASB}}} \end{array}\)
Theo giá thuyết: \(\left| {\overrightarrow {SB} } \right| = \left| {\overrightarrow {SC} } \right|\)
Và: \(c{\rm{os}}\widehat {{\rm{CSA}}} = c{\rm{os}}\widehat {{\rm{ASB}}} \Rightarrow \overrightarrow {SA} .\overrightarrow {BC} = 0\)
Vậy: \(SA \bot BC.\)
Chứng minh tương tự ta có: \(SB\bot AC, SC \bot AB.\)
Ví dụ 2:
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Tính số đo của góc giữa (BA’C) và (DA’C).
Hướng dẫn giải:
.png)
Kẻ \(BH \bot A'C,{\rm{ (H}} \in {\rm{A'C)}}\) (1).
Mặt khác: \(BD \bot AC{\rm{ (gt)}}\)
\(AA' \bot (ABCD) \Rightarrow AA' \bot BD{\rm{ }}\)
\(\Rightarrow BD \bot (ACA') \Rightarrow BD \bot A'C\) (2)
Từ (1) (2) suy ra:
\(A'C \bot (BDH) \Rightarrow A'C \bot DH\)
Do đó: \((\widehat {(BA'C),(DA'C)}) = (\widehat {HB,HD})\)
Xét tam giác BCA' ta có:
\(\frac{1}{{B{H^2}}} = \frac{1}{{B{C^2}}} + \frac{1}{{BA{'^2}}} = \frac{3}{{2{a^2}}} \Rightarrow BH = a.\sqrt {\frac{2}{3}} \Rightarrow DH = a.\sqrt {\frac{2}{3}}\)
Ta có:
\(\cos \widehat {BHD} = \frac{{2B{H^2} - B{D^2}}}{{2B{H^2}}} = - \frac{1}{2} \Rightarrow \widehat {BHD} = {120^0}>90^0\)
Vậy: \(\widehat {((BA'C),(DA'C))} =180^0-120^0= {60^0}.\)
Ví dụ 3:
Cho hình lăng trụ đứng ABC.A’B’C’, đáy ABC là tam giác cân AB=AC=a, \(\widehat {BAC} = {120^0}\), BB’=a, I là trung điểm của CC’. Tính cosin của góc giữa hai mp(ABC) và (AB’I).
Hướng dẫn giải:
.png)
Ta thấy tam giác ABC là hình chiếu vuông góc của tam giác AB’I lên mặt phẳng (ABC).
Gọi φ là góc giữa hai mặt phẳng (ABC) và (AB’I).
Theo công thức hình chiếu ta có: \(\cos \varphi = \frac{{{S_{ABC}}}}{{{S_{AB'I}}}}\).
Ta có:
\({S_{ABC}} = \frac{1}{2}.AB.AC.\sin {120^0} = \frac{{{a^2}\sqrt 3 }}{4}\)
\(AI = \sqrt {A{C^2} + C{I^2}} = \frac{{a\sqrt 5 }}{2}\)
\(AB' = \sqrt {A{B^2} + BB{'^2}} = a\sqrt 2\)
\(IB' = \sqrt {B'C{'^2} + IC{'^2}} = \frac{{a\sqrt {13} }}{2}.\)
Suy ra: Tam giác AB’I vuông tại A nên \({S_{AB'I}} = \frac{1}{2}.AB'.AI = \frac{{{a^2}\sqrt {10} }}{4}\).
Vậy: \(\cos \varphi = \frac{{{S_{ABC}}}}{{{S_{AB'I}}}} = \sqrt {\frac{3}{{10}}} .\)
Ví dụ 4:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA = SB = SC = SD = \(a\sqrt2\). Tính khoảng cách giữa hai đường thẳng chéo nhau AD và SC.
Hướng dẫn giải:

Hướng dẫn giải:
Vì AD // BC nên d(AD, SC) = d(AD, (SBC)) = d(A, (SBC)).
Ta có \(AO\cap (SBC)=C\) và \(\frac{CO}{CA}=\frac{1}{2}\), do đó:
d(A,(SBC)) = 2.d(O,(SBC)).
\(SO \bot (ABCD)\) nên \(SO \bot BC\)
Kẻ \(SI \bot BC\) thì I là trung điểm của BC.
Suy ra: \(BC \bot (SOI)\Rightarrow (SBC)\bot (SOI)\)
\((SBC)\cap (SOI)=SI\)
Kẻ \(OI \bot SI (H\in SI).\) Khi đó \(d(O,(SBC)) = OH\)
Xét tam giác SOI vuông tại O, theo hệ thức lượng trong tam giác vuông ta có:
\(\frac{1}{{O{H^2}}} = \frac{1}{{O{J^2}}} + \frac{1}{{O{S^2}}}\) mà \(OJ = \frac{1}{2}.a;\,\,SO = \sqrt {S{C^2} - C{O^2}} = \frac{{a\sqrt 6 }}{2}\)
Suy ra: \(OH = \frac{{\sqrt {42} }}{{14}}a.\)
Vậy: \(d(AD,SC) = 2.\frac{{\sqrt {42} }}{{14}}a = \frac{{\sqrt {42} }}{7}.a.\)
Lời kết
Trên đây, bài viết đã giới thiệu đến các em những nội dung kiến thức trọng tâm của Hình học 11.Để cũng cố kiến thức và rèn luyện kĩ năng giải bài tập, xin mời các em cũng làm bài kiểm tra Trắc nghiệm Hình học 11 với những câu hỏi củng cố bám sát chương trình. Bên cạnh đó các em có thể nêu thắc mắc của mình thông qua phần Hỏi - đáp cộng đồng Toán HỌC247 sẽ sớm giải đáp cho các em.
Bên cạnh đó các em có thể xem phần hướng dẫn Giải bài tập SGK sẽ giúp các em nắm được các phương pháp giải bài tập từ SGK Hình học Cơ bản và Nâng cao.
-- Mod Toán Học 11 HỌC247





.PNG)






