Trong quá trình học bài Giới hạn của hàm số, nếu các em gặp những thắc mắc cần giài đáp hay những bài tập không biết phương pháp giải từ SGK, Sách tham khảo, Các trang mạng,... Các em hãy đặt câu hỏi ở đây cộng đồng Toán HỌC247 sẽ sớm giải đáp cho các em.
Danh sách hỏi đáp (308 câu):
-
Tính giới hạn sau: \(\mathop {\lim }\limits_{x \to + \infty } {{x - 1} \over {{x^2} - 1}}\)
28/02/2021 | 1 Trả lời
Theo dõi (0)Gửi câu trả lời Hủy -
Tính giới hạn sau: \(\mathop {\lim }\limits_{x \to - 3} {{x + 3} \over {{x^2} + 2x - 3}}\)
01/03/2021 | 1 Trả lời
Theo dõi (0)Gửi câu trả lời Hủy -
Tìm giới hạn của hàm số sau: \(h\left( x \right) = {{x - 15} \over {x + 2}}\) khi \(x \to - {2^ + }\) và khi \(x \to - {2^ - }\)
01/03/2021 | 1 Trả lời
Theo dõi (0)Gửi câu trả lời Hủy -
Tìm giới hạn của hàm số sau: \(k\left( x \right) = \sqrt {4{x^2} - x + 1} \) khi \(x \to - \infty \)
01/03/2021 | 1 Trả lời
Theo dõi (0)Gửi câu trả lời Hủy -
Tìm giới hạn của hàm số sau: \(h\left( x \right) = {{2{x^3} + 15} \over {{{\left( {x + 2} \right)}^2}}}\) khi \(x \to - 2\)
01/03/2021 | 1 Trả lời
Theo dõi (0)Gửi câu trả lời Hủy -
Tìm giới hạn của hàm số sau: \(f\left( x \right) = {{{x^2} - 2x - 3} \over {x - 1}}\) khi \(x \to 3\)
28/02/2021 | 1 Trả lời
Theo dõi (0)Gửi câu trả lời Hủy -
Cho hai hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) cùng xác định trên khoảng \(\left( { - \infty ,a} \right)\). Dùng định nghĩa chứng minh rằng, nếu \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = L\) và \(\mathop {\lim }\limits_{x \to - \infty } g\left( x \right) = M\) thì \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right).g\left( x \right) = L.M\).
01/03/2021 | 1 Trả lời
Theo dõi (0)Gửi câu trả lời Hủy -
Chứng minh rằng hàm số \(y = \sin x\) không có giới hạn khi \(x \to + \infty \).
01/03/2021 | 1 Trả lời
Theo dõi (0)Gửi câu trả lời Hủy -
Dùng định nghĩa tìm giới hạn: \(\mathop {\lim }\limits_{x \to + \infty } {{{x^3} + 1} \over {{x^2} + 1}}\)
28/02/2021 | 1 Trả lời
Theo dõi (0)Gửi câu trả lời Hủy -
Dùng định nghĩa tìm giới hạn: \(\mathop {\lim }\limits_{x \to 5} {{x + 3} \over {3-x}}\).
28/02/2021 | 1 Trả lời
Theo dõi (0)Gửi câu trả lời Hủy -
Tinh giới hạn của các hàm số sau
28/02/2021 | 0 Trả lời
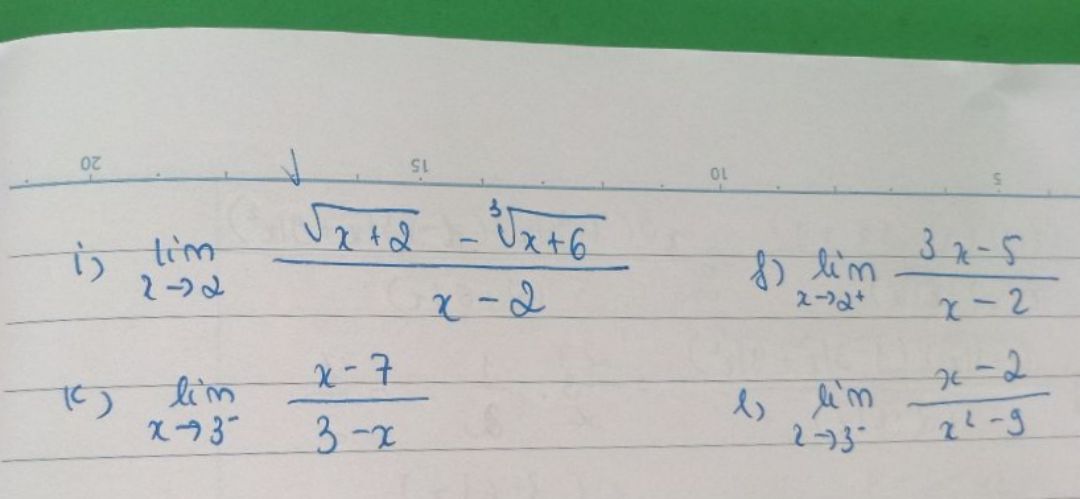Theo dõi (0)Gửi câu trả lời Hủy -
Tính: \(\eqalign{&\mathop {\lim }\limits_{x \to + \infty } {{\sqrt {{x^2} + 1} + x} \over {5 - 2x}} \cr} \)
23/02/2021 | 1 Trả lời
Theo dõi (0)Gửi câu trả lời Hủy -
Tính: \(\eqalign{&\mathop {\lim }\limits_{x \to - \infty } (\sqrt {{x^2} - 2x + 5}) \cr } \)
24/02/2021 | 1 Trả lời
Theo dõi (0)Gửi câu trả lời Hủy -
Tính: \(\eqalign{& & \mathop {\lim }\limits_{x \to - \infty } ( - 2{x^3} + 3{x^2} - 5) \cr }\)
23/02/2021 | 1 Trả lời
Theo dõi (0)Gửi câu trả lời Hủy -
Tính: \(\eqalign{& \mathop {\lim }\limits_{x \to + \infty } ({x^4} - {x^2} + x - 1) \cr} \)
24/02/2021 | 1 Trả lời
Theo dõi (0)Gửi câu trả lời Hủy -
Tính giới hạn sau: \(\underset{x\rightarrow 1^{+}}{lim}\) \(\frac{2x -7}{x-1}\)
23/02/2021 | 1 Trả lời
Theo dõi (0)Gửi câu trả lời Hủy -
Tính giới hạn sau: \(\underset{x\rightarrow 1^{-}}{lim}\) \(\frac{2x -7}{x-1}\)
24/02/2021 | 1 Trả lời
Theo dõi (0)Gửi câu trả lời Hủy -
Tính giới hạn sau: \(\underset{x\rightarrow 2}{lim}\) \(\frac{3x -5}{(x-2)^{2}}\)
24/02/2021 | 1 Trả lời
Theo dõi (0)Gửi câu trả lời Hủy -
Tính giới hạn sau: \(\underset{x\rightarrow +\infty }{\lim}\) \(\dfrac{-2x^{2}+x -1}{3 +x}\)
23/02/2021 | 1 Trả lời
Theo dõi (0)Gửi câu trả lời Hủy -
Tính giới hạn sau: \(\underset{x\rightarrow +\infty }{\lim}\) \(\dfrac{17}{x^{2}+1}\)
23/02/2021 | 1 Trả lời
Theo dõi (0)Gửi câu trả lời Hủy -
Tính giới hạn sau: \(\underset{x\rightarrow +\infty }{\lim}\) \(\dfrac{2x-6}{4-x}\)
23/02/2021 | 1 Trả lời
Theo dõi (0)Gửi câu trả lời Hủy -
Tính giới hạn sau: \(\underset{x\rightarrow 6}{\lim}\) \(\dfrac{\sqrt{x + 3}-3}{x-6}\)
23/02/2021 | 1 Trả lời
Theo dõi (0)Gửi câu trả lời Hủy -
Tính giới hạn sau: \(\underset{x\rightarrow -2}{\lim}\) \(\dfrac{4-x^{2}}{x + 2}\)
23/02/2021 | 1 Trả lời
Theo dõi (0)Gửi câu trả lời Hủy -
Tính giới hạn sau: \(\underset{x\rightarrow -3}{\lim}\) \(\frac{x^{2 }-1}{x+1}\)
23/02/2021 | 1 Trả lời
Theo dõi (0)Gửi câu trả lời Hủy -
Cho hàm số \(f(x) = \left\{ \matrix{ \sqrt x + 1 \text{ nếu }x\ge 0 \hfill \cr 2x\text{ nếu }x < 0 \hfill \cr} \right.\) Và các dãy số \((u_n)\) với \(u_n= \dfrac{1}{n}\), \((v_n)\) với \(v_n= -\dfrac{1}{n}\). Tính \(\lim u_n\), \(\lim v_n\), \(\lim f (u_n)\) và \(\lim f(v_n)\).
24/02/2021 | 1 Trả lời
Theo dõi (0)Gửi câu trả lời Hủy
