Trong quá trình học bài Giới hạn của hàm số, nếu các em gặp những thắc mắc cần giài đáp hay những bài tập không biết phương pháp giải từ SGK, Sách tham khảo, Các trang mạng,... Các em hãy đặt câu hỏi ở đây cộng đồng Toán HỌC247 sẽ sớm giải đáp cho các em.
Danh sách hỏi đáp (308 câu):
-
Dùng định nghĩa tìm giới hạn sau: \(\mathop {\lim }\limits_{x \to + \infty } {{{x^3} + 1} \over {{x^2} + 1}}\)
26/04/2022 | 1 Trả lời
Theo dõi (0)Gửi câu trả lời Hủy -
Dùng định nghĩa tìm giới hạn sau: \(\mathop {\lim }\limits_{x \to 5} {{x + 3} \over {3-x}}\)
26/04/2022 | 1 Trả lời
Theo dõi (0)Gửi câu trả lời Hủy -
Tính các giới hạn sau: lim3n3+2n+5/1+2n5
05/05/2021 | 2 Trả lời
lim3n3+2n+5/1+2n5
Theo dõi (1)Gửi câu trả lời Hủy -
khó
Theo dõi (0)Gửi câu trả lời Hủy -
Tính các giới hạn của hàm số
15/03/2021 | 0 Trả lời
Giúp vs ạ
Theo dõi (1)Gửi câu trả lời Hủy -
Tính giới hạn của hàm số lượng giác
13/03/2021 | 1 Trả lời
Theo dõi (0)Gửi câu trả lời Hủy -
Tìm giới hạn lim x-căn x 2/căn 4x 1 -3
07/03/2021 | 0 Trả lời
tìn giới hạn lim x-căn x 2/căn 4x 1 -3Theo dõi (0)Gửi câu trả lời Hủy -
Tính giới hạn của hàm số
04/03/2021 | 0 Trả lời
Giúp mình câu 8 với ạ!!
Theo dõi (0)Gửi câu trả lời Hủy -
Tính giới hạn của hàm số
03/03/2021 | 1 Trả lời
Giúp em với ạ. Em cảm ơn ạ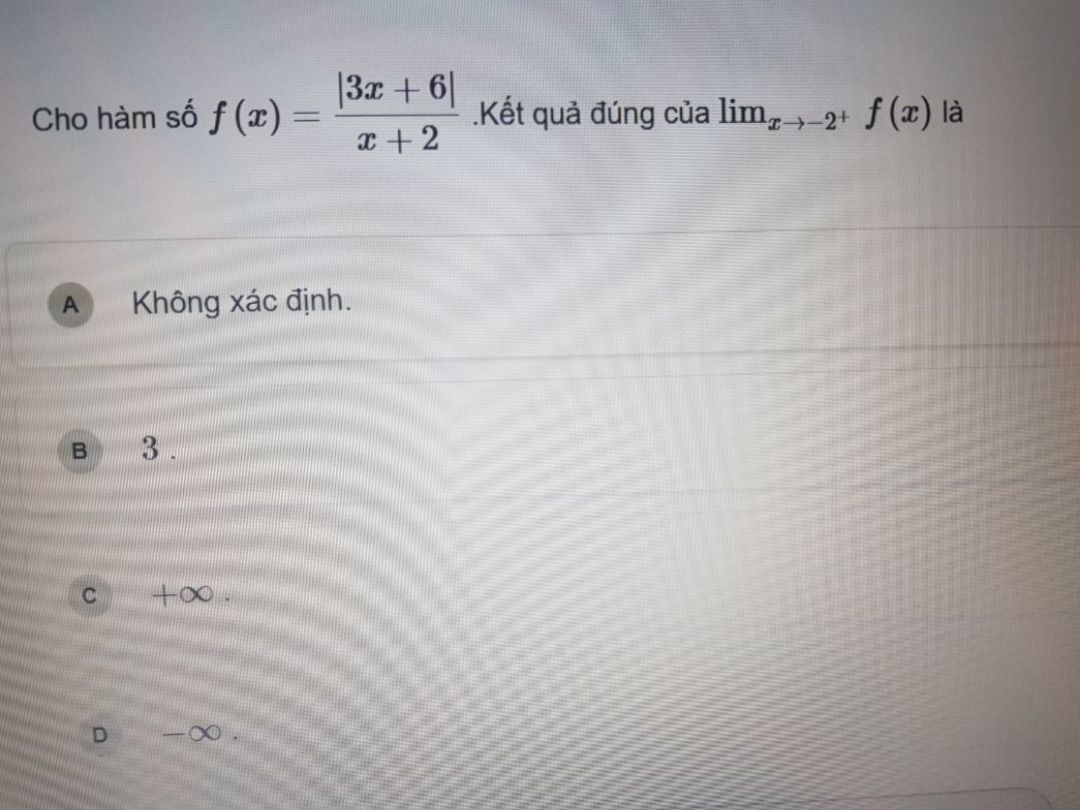
Theo dõi (0)Gửi câu trả lời Hủy -
Cho hàm số \(y = f\left( x \right)\) xác định trên khoảng \(\left( {a; + \infty } \right)\). Chứng minh rằng nếu \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = - \infty \) thì luôn tồn tại ít nhất một số c thuộc \(\left( {a; + \infty } \right)\) sao cho \(f\left( c \right) < 0\)
28/02/2021 | 1 Trả lời
Theo dõi (0)Gửi câu trả lời Hủy -
Cho khoảng \(K,{x_0} \in K\) và hàm số \(y = f\left( x \right)\) xác định trên \(K\backslash \left\{ {{x_0}} \right\}\). Chứng minh rằng nếu \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = + \infty \) thì luôn tồn tại ít nhất một số c thuộc \(K\backslash \left\{ {{x_0}} \right\}\) sao cho \(f\left( c \right) > 0\)
01/03/2021 | 1 Trả lời
Theo dõi (0)Gửi câu trả lời Hủy -
Tính giới hạn của hàm số sau khi \(x \to + \infty \) và khi \(x \to - \infty \): \(f\left( x \right) = \sqrt {{x^2} - x} - \sqrt {{x^2} + 1} \)
01/03/2021 | 1 Trả lời
Theo dõi (0)Gửi câu trả lời Hủy -
Tính giới hạn của hàm số sau khi \(x \to + \infty \) và khi \(x \to - \infty \): \(f\left( x \right) = x + \sqrt {{x^2} - x + 1}\)
01/03/2021 | 1 Trả lời
Theo dõi (0)Gửi câu trả lời Hủy -
Tính giới hạn của hàm số sau khi \(x \to + \infty \) và khi \(x \to - \infty \): \(f\left( x \right) = {{\sqrt {{x^2} - 3x} } \over {x + 2}}\)
01/03/2021 | 1 Trả lời
Theo dõi (0)Gửi câu trả lời Hủy -
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}mx + 2\,neu\,x \le 1\\\dfrac{1}{{x - 1}} - \dfrac{3}{{{x^3} - 1}}\,neu\,x > 1\end{array} \right.\). Với giá trị nào của tham số m thì hàm số f(x) có giới hạn khi x → 1?
01/03/2021 | 1 Trả lời
A. m = -1
B. m = 1
C. m = -2
D. m = 2
Theo dõi (0)Gửi câu trả lời Hủy -
\(\mathop {\lim }\limits_{x \to - \infty } \dfrac{{2{x^4} + 15x + 6}}{{{x^3} - 5x + 2}}\) bằng:
28/02/2021 | 1 Trả lời
A. 2
B. 3
C. +∞
D. -∞
Theo dõi (0)Gửi câu trả lời Hủy -
\(\mathop {\lim }\limits_{x \to - 2} \dfrac{{\sqrt {{x^2} + 5} - 3}}{{x + 2}}\) bằng:
01/03/2021 | 1 Trả lời
A. 0
B. 1
C. -2/3
D. -∞
Theo dõi (0)Gửi câu trả lời Hủy -
\(\mathop {\lim }\limits_{x \to 0} \dfrac{{{{\left( {1 + x} \right)}^3} - 1}}{x}\) bằng:
28/02/2021 | 1 Trả lời
A. 0
B. 1
C. 3
D. +∞
Theo dõi (0)Gửi câu trả lời Hủy -
\(\mathop {\lim }\limits_{x \to - \infty } \left( {{x^3} + {x^2} + 1} \right)\) bằng:
01/03/2021 | 1 Trả lời
A. 1
B. +∞
C. -∞
D. -1
Theo dõi (0)Gửi câu trả lời Hủy -
Tính giới hạn sau: \(\mathop {\lim }\limits_{x \to - \infty } {{\left( {{x^2} - 1} \right){{\left( {1 - 2x} \right)}^5}} \over {{x^7} + x + 3}}\)
01/03/2021 | 1 Trả lời
Theo dõi (0)Gửi câu trả lời Hủy -
Tính giới hạn sau: \(\mathop {\lim }\limits_{x \to 0} {1 \over {{x^2}}}\left( {{1 \over {{x^2} + 1}} - 1} \right)\)
01/03/2021 | 1 Trả lời
Theo dõi (0)Gửi câu trả lời Hủy -
Tính giới hạn sau: \(\mathop {\lim }\limits_{x \to + \infty } {{1 - 2x + 3{x^3}} \over {{x^3} - 9}}\)
01/03/2021 | 1 Trả lời
Theo dõi (0)Gửi câu trả lời Hủy -
Tính giới hạn sau: \(\mathop {\lim }\limits_{x \to 1} {{\sqrt x - 1} \over {\sqrt {x + 3} - 2}}\)
01/03/2021 | 1 Trả lời
Theo dõi (0)Gửi câu trả lời Hủy -
Tính giới hạn sau: \(\mathop {\lim }\limits_{x \to + \infty } {{x - 5} \over {\sqrt x + \sqrt 5 }}\)
01/03/2021 | 1 Trả lời
Theo dõi (0)Gửi câu trả lời Hủy -
Tính giới hạn sau: \(\mathop {\lim }\limits_{x \to 5} {{x - 5} \over {\sqrt x - \sqrt 5 }}\)
01/03/2021 | 1 Trả lời
Theo dõi (0)Gửi câu trả lời Hủy
