Bài tập 4 trang 78 SGK Hình học 11 NC

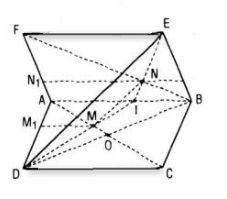
a) Gọi O là tâm hình bình hành ABCD, ta có AO là trung tuyến và \(\frac{{AM}}{{AO}} = \frac{{2AM}}{{AC}} = \frac{2}{3}\)

⇒ M là trọng tâm của tam giác ABD , tương tự N là trọng tâm tam giác ABE

Gọi I là trung điểm của AB thì M, N lần lượt trên DI và EI

Trong tam giác IDE ta có: 

\(\frac{{IM}}{{ID}} = \frac{{IN}}{{IE}} = \frac{1}{3}\) nên MN // DE và \(MN = \frac{1}{3}DE\)

b) Trong ∆FAB: NN₁ // AB

\( \Rightarrow \frac{{A{N_1}}}{{AF}} = \frac{{BN}}{{BF}} = \frac{1}{3}\)

Trong ∆DAB: MM1 // AB

\( \Rightarrow \frac{{A{M_1}}}{{AD}} = \frac{{DM}}{{DI}} = \frac{1}{3}\)

Do đó \(\frac{{A{N_1}}}{{AF}} = \frac{{A{M_1}}}{{AD}}\) nên M₁N₁ // DF

Mà DF ⊂ (DEF) suy ra M₁N₁ // mp(DEF)

c) Ta có : M₁N₁ // DF, NN₁ // EF

Mà M₁N₁ và NN₁ cắt nhau và nằm trong mp(MNN₁M₁), còn DF và EF cắt nhau và nằm trong mp(DEF)

Vậy mp(MNN₁M₁) // mp(DEF).

-- Mod Toán 11 HỌC247