Bài tập 7.15 trang 30 SBT Toán 11 Tập 2 Kết nối tri thức - KNTT

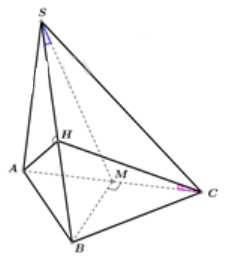
a) Gọi \(M\) là trung điểm đoạn \(AC\) thì \(BM \bot AC \Rightarrow BM \bot \left( {SAC} \right) \Rightarrow SM\) là hình chiếu vuông góc của \(SB\) lên mặt phẳng \(\left( {SAC} \right)\).

Khi đó \(\left( {\widehat {SB,\left( {SAC} \right)}} \right) = \left( {\widehat {SB,SM}} \right) = \widehat {BSM}\).

Tam giác \(SBM\) vuông tại \(M\) có \(BM = AM = \frac{1}{2}AC = \frac{{a\sqrt 2 }}{2}\) và \(SM = \sqrt {S{A^2} + A{M^2}} = \frac{{a\sqrt {26} }}{2}\)

Do đó \(\tan \widehat {BSM} = \frac{{BM}}{{SM}} = \frac{{\sqrt {13} }}{{13}}\).

b) Trong mp\(\left( {SAB} \right)\), kẻ \(AH \bot SB\) thì \(AH \bot \left( {SBC} \right)\) (vì \(AH \bot SB,AH \bot BC\)).

Khi đó \(HC\) là hình chiếu vuông góc của \(AC\) lên mp\(\left( {SBC} \right)\).

Suy ra \(\left( {\widehat {AC,\left( {SBC} \right)}} \right) = \left( {\widehat {AC,HC}} \right) = \widehat {ACH}\).

Mặt khác tam giác \(AHC\) vuông tại \(H\) có \(AC = a\sqrt 2 \) và \(AH = \frac{{SA.AB}}{{\sqrt {S{A^2} + A{B^2}} }} = \frac{{a\sqrt {42} }}{7}\).

Do đó \(\sin \widehat {ACH} = \frac{{AH}}{{AC}} = \frac{{\sqrt {21} }}{7}\).

-- Mod Toán 11 HỌC247