Chuy√™n ƒë·ªÅ Chuy√™n ƒë·ªÅ S·ª± ch·ªìng ch·∫•t ƒëi·ªán tr∆∞·ªùng - ƒêi·ªán tr∆∞·ªùng t·ªïng h·ª£p m√¥n V·∫≠t L√Ω 11 nƒÉm 2021 d∆∞·ªõi ƒë√¢y t·ªïng h·ª£p l·∫°i nh·ªØng ki·∫øn th·ª©c quan tr·ªçng ƒë√£ h·ªçc, qua ƒë√≥ gi√∫p c√°c em c√≥ th·ªÉ t·ª± luy·ªán t·∫≠p v√Ý tham kh·∫£o th√™m. Hy v·ªçng ƒë√¢y s·∫Ω l√Ý t√Ýi li·ªáu h·ªØu √≠ch gi√∫p c√°c em √¥n t·∫≠p t·ªët ki·∫øn th·ª©c, chu·∫©n b·ªã h√Ýnh trang s·∫µn s√Ýng cho k√¨ thi s·∫Øp t·ªõi c·ªßa m√¨nh. M·ªùi c√°c em c√πng tham kh·∫£o!
CHUYÊN ĐỀ SỰ CHỒNG CHẤT ĐIỆN TRƯỜNG
- ĐIỆN TRƯỜNG TỔNG HỢP
1. PH∆Ø∆ÝNG PH√ÅP GI·∫¢I
G·ªçi \(\overrightarrow{{{E}_{1}}},\overrightarrow{{{E}_{2}}},\overrightarrow{{{E}_{3}}},...\) l√Ý ƒëi·ªán tr∆∞·ªùng do ƒëi·ªán t√≠ch \({{q}_{1}},{{q}_{2}},{{q}_{3}},...\) g√¢y ra t·∫°i ƒëi·ªÉm M.
C∆∞·ªùng ƒë·ªô ƒëi·ªán tr∆∞·ªùng t·ªïng h·ª£p t·∫°i M do \({{q}_{1}},{{q}_{2}},{{q}_{3}},...\) g√¢y ra l√Ý:
\({\overrightarrow E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} + \overrightarrow {{E_3}} + ...}\)
Thông thường ta sẽ gặp hai hoặc ba điện tích gây ra điện trường tại điểm M.
Cường độ điện trường được tính bằng công thức sau:
\(E=k.\frac{\left| Q \right|}{{{r}^{2}}}=\frac{F}{q}\)
2. BÀI TẬP VÍ DỤ
V√≠ d·ª• 1: Trong ch√¢n kh√¥ng, m·ªôt ƒëi·ªán t√≠ch ƒëi·ªÉm \(q={{2.10}^{-8}}\text{C}\) ƒë·∫∑t t·∫°i m·ªôt ƒëi·ªÉm M trong ƒëi·ªán tr∆∞·ªùng c·ªßa m·ªôt ƒëi·ªán t√≠ch ƒëi·ªÉm \(Q={{2.10}^{-6}}\text{C}\) ch·ªãu t√°c d·ª•ng c·ªßa m·ªôt l·ª±c ƒëi·ªán \(F={{9.10}^{-3}}\text{ N}\). T√≠nh c∆∞·ªùng ƒë·ªô ƒëi·ªán tr∆∞·ªùng t·∫°i M v√Ý kho·∫£ng c√°ch gi·ªØa hai ƒëi·ªán t√≠ch?
A. \({{\text{E}}_{M}}={{90.10}^{4}}\left( \text{V/m} \right),\,\,r=0,141\,\left( \text{m} \right).\)
B. \({{\text{E}}_{M}}=45\sqrt{2}{{.10}^{4}}\left( \text{V/m} \right),\,\,r=0,17\,\left( \text{m} \right).\)
C. \({{\text{E}}_{M}}={{45.10}^{4}}\left( \text{V/m} \right),\,\,r=0,2\,\left( \text{m} \right).\)
D. \({{\text{E}}_{M}}=45\sqrt{3}{{.10}^{4}}\left( \text{V/m} \right),\,\,r=0,15\,\left( \text{m} \right).\)
L·ªùi gi·∫£i
C∆∞·ªùng ƒë·ªô ƒëi·ªán tr∆∞·ªùng t·∫°i M l√Ý \(E=k.\frac{\left| Q \right|}{{{r}^{2}}}=\frac{F}{q}={{45.10}^{4}}\left( \text{V/m} \right)\)
Khoảng cách giữa hai điện tích xác định bởi \(r=\sqrt{\frac{k\left| Q \right|}{E}}=0,2\left( \text{m} \right)\)
Đáp án C.
V√≠ d·ª• 2: Trong ch√¢n kh√¥ng c√≥ hai ƒëi·ªán t√≠ch ƒëi·ªÉm \({{q}_{1}}={{2.10}^{-8}}C,\text{ }{{q}_{2}}=-{{32.10}^{-8}}\text{C}\) ƒë·∫∑t t·∫°i hai ƒëi·ªÉm A v√Ý B c√°ch nhau m·ªôt kho·∫£ng 30 cm. X√°c ƒë·ªãnh v·ªã tr√≠ ƒëi·ªÉm M t·∫°i ƒë√≥ c∆∞·ªùng ƒë·ªô ƒëi·ªán tr∆∞·ªùng b·∫±ng kh√¥ng.
A. M l√Ý trung ƒëi·ªÉm c·ªßa AB.
B. M n·∫±m tr√™n ƒë∆∞·ªùng th·∫≥ng AB v√Ý n·∫±m ngo√Ýi ƒëo·∫°n AB, th·ªèa m√£n \(MA=10\text{ cm},\text{ }MB=40\text{ cm}\).
C. M n·∫±m tr√™n ƒë∆∞·ªùng th·∫≥ng AB v√Ý n·∫±m ngo√Ýi ƒëo·∫°n AB, th·ªèa m√£n \(MA=40\text{ cm},\text{ }MB=10\text{ cm}\).
D. M n·∫±m tr√™n ƒë∆∞·ªùng th·∫≥ng AB v√Ý n·∫±m trong ƒëo·∫°n AB, th·ªèa m√£n \(MA=10\text{ cm},\text{ }MB=20\text{ cm}\).
L·ªùi gi·∫£i
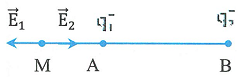
C∆∞·ªùng ƒë·ªô ƒëi·ªán tr∆∞·ªùng t·∫°i M l√Ý \(\overrightarrow{{{E}_{M}}}=\overrightarrow{{{E}_{1}}}+\overrightarrow{{{E}_{2}}}=\vec{0}\Rightarrow \overrightarrow{{{E}_{1}}}=-\overrightarrow{{{E}_{2}}}\), m·∫∑t kh√°c 2 ƒëi·ªán t√≠ch ƒëi·ªÉm tr√°i d·∫•u v·ªõi nhau n√™n t·ª´ ƒë√¢y suy ra ƒë∆∞·ª£c M ph·∫£i n·∫±m ngo√Ýi ƒëo·∫°n AB (h√¨nh v·∫Ω). Ta c√≥:
\({{E}_{1}}={{E}_{2}}\Rightarrow \frac{\left| {{q}_{1}} \right|}{M{{A}^{2}}}=\frac{\left| {{q}_{2}} \right|}{M{{B}^{2}}}\Rightarrow \frac{M{{B}^{2}}}{M{{A}^{2}}}=\frac{32}{2}=16\Rightarrow MB=4MA\) \(\left( 1 \right)\)
V√¨ M n·∫±m ngo√Ýi AB n√™n \(MB-MA=30\left( \text{cm} \right)\) \(\left( 2 \right)\)
T·ª´ \(\left( 1 \right)\) v√Ý \(\left( 2 \right)\) \(\Rightarrow MA=10\text{ cm},\text{ }MB=40\text{ cm}\)
Đáp án B.
3. BÀI TẬP TRẮC NGHIỆM
C√¢u 1: Hai ƒëi·ªán t√≠ch ƒëi·ªÉm \({{q}_{1}}=5nC,\text{ }{{q}_{2}}=-5nC\) c√°ch nhau 10cm. X√°c ƒë·ªãnh v√©ct∆° c∆∞·ªùng ƒë·ªô ƒëi·ªán tr∆∞·ªùng t·∫°i ƒëi·ªÉm M n·∫±m tr√™n ƒë∆∞·ªùng th·∫≥ng ƒëi qua hai ƒëi·ªán t√≠ch ƒë√≥ v√Ý c√°ch ƒë·ªÅu hai ƒëi·ªán t√≠ch:
A. 18000 V/m
B. 45000 V/m
C. 36000 V/m
D. 12500 V/m
C√¢u 2: Hai ƒëi·ªán t√≠ch ƒëi·ªÉm \({{q}_{1}}=5nC,\text{ }{{q}_{2}}=-5nC\)c√°ch nhau 10cm. X√°c ƒë·ªãnh v√©ct∆° c∆∞·ªùng ƒë·ªô ƒëi·ªán tr∆∞·ªùng t·∫°i ƒëi·ªÉm M n·∫±m tr√™n ƒë∆∞·ªùng th·∫≥ng ƒëi qua hai ƒëi·ªán t√≠ch ƒë√≥ v√Ý c√°ch \({{q}_{1}}\) 5cm; c√°ch \({{q}_{2}}\) 15cm:
A. 4500 V/m
B. 36000 V/m
C. 18000 V/m
D. 16000 V/m
C√¢u 3: T·∫°i ba ƒë·ªânh c·ªßa tam gi√°c ƒë·ªÅu c·∫°nh 10cm c√≥ ba ƒëi·ªán t√≠ch b·∫±ng nhau v√Ý b·∫±ng 10nC. H√£y x√°c ƒë·ªãnh c∆∞·ªùng ƒë·ªô ƒëi·ªán tr∆∞·ªùng t·∫°i trung ƒëi·ªÉm c·ªßa c·∫°nh BC c·ªßa tam gi√°c:
A. 2100 v/m
B. 6800 V/m
C. 9700 V/m
D. 12 000 V/m
C√¢u 4: T·∫°i ba ƒë·ªânh c·ªßa tam gi√°c ƒë·ªÅu c·∫°nh 10cm c√≥ ba ƒëi·ªán t√≠ch b·∫±ng nhau v√Ý b·∫±ng 10 nC. H√£y x√°c ƒë·ªãnh c∆∞·ªùng ƒë·ªô ƒëi·ªán tr∆∞·ªùng t·∫°i t√¢m c·ªßa tam gi√°c:
A. 0
B. 1200 V/m
C. 2400 V/m
D. 3600 V/m
C√¢u 5: M·ªôt ƒëi·ªán t√≠ch ƒëi·ªÉm \(q=2,5\text{ }\!\!\mu\!\!\text{ C}\) ƒë·∫∑t t·∫°i ƒëi·ªÉm M trong ƒëi·ªán tr∆∞·ªùng ƒë·ªÅu m√Ý ƒëi·ªán tr∆∞·ªùng c√≥ hai th√Ýnh ph·∫ßn \({{\text{E}}_{x}}=+6000\text{V/m}\), \({{\text{E}}_{y}}=-6\sqrt{3}\text{.1}{{\text{0}}^{3}}\,\,\text{V/m}\). V√©ct∆° l·ª±c t√°c d·ª•ng l√™n ƒëi·ªán t√≠ch q l√Ý:
A. \(F=0,03\text{N}\), lập với trục Oy một góc \(\text{15}{{\text{0}}^{0}}\)
B. \(F=0,3\text{N}\), lập với trục Oy một góc \({{30}^{0}}\)
C. \(F=0,03\text{N}\), lập với trục Oy một góc \({{115}^{0}}\)
D. \(F=0,12\text{N}\), lập với trục Oy một góc \({{120}^{0}}\)
Câu 6: Ba điện tích điểm cùng độ lớn, cùng dấu q đặt tại ba đỉnh của một tam giác đều cạnh a. Xác định cường độ điện trường tại điểm đặt của mỗi điện tích do hai điện tích kia gây ra:
A. \(E=k\frac{2q\sqrt{2}}{{{a}^{2}}}\)
B. \(E=2k\frac{q\sqrt{3}}{{{a}^{2}}}\)
C. \(E=k\frac{q\sqrt{3}}{{{a}^{2}}}\)
D. \(E=k\frac{q\sqrt{3}}{a}\)
Câu 7: Hai điện tích điểm cùng độ lớn q, trái dấu, đặt tại 2 đỉnh của một tam giác đều cạnh a. Xác định cường độ điện trường tại đỉnh còn lại của tam giác do hai điện tích kia gây ra:
A. \(E=k\frac{q}{{{a}^{2}}}\)
B. \(E=k\frac{q\sqrt{3}}{{{a}^{2}}}\)
C. \(E=2k\frac{q}{{{a}^{2}}}\)
D. \(E=\frac{1}{2}k\frac{q}{{{a}^{2}}}\)
Câu 8: Bốn điện tích điểm cùng độ lớn cùng dấu q đặt tại bốn đỉnh của hình vuông cạnh a. Xác định cường độ điện trường gây ra bởi bốn điện tích đó tại tâm của hình vuông:
A. \(E=2k\frac{q}{{{a}^{2}}}\)
B. \(E=4k\frac{q\sqrt{2}}{{{a}^{2}}}\)
C. 0
D. \(E=k\frac{q\sqrt{3}}{{{a}^{2}}}\)
C√¢u 9: B·ªën ƒëi·ªán t√≠ch ƒëi·ªÉm c√πng ƒë·ªô l·ªõn q, hai ƒëi·ªán t√≠ch d∆∞∆°ng v√Ý hai ƒëi·ªán t√≠ch √¢m, ƒë·∫∑t t·∫°i b·ªën ƒë·ªânh c·ªßa h√¨nh vu√¥ng c·∫°nh a, c√°c ƒëi·ªán t√≠ch c√πng d·∫•u k·ªÅ nhau. X√°c ƒë·ªãnh c∆∞·ªùng ƒë·ªô ƒëi·ªán tr∆∞·ªùng g√¢y ra b·ªüi b·ªën ƒëi·ªán t√≠ch ƒë√≥ t·∫°i t√¢m c·ªßa h√¨nh vu√¥ng:
A. \(E=2k\frac{q\sqrt{3}}{{{a}^{2}}}\)
B. \(E=k\frac{q\sqrt{3}}{{{a}^{2}}}\)
C. \(E=k\frac{q\sqrt{3}}{2{{a}^{2}}}\)
D. \(E=4k\frac{q\sqrt{2}}{{{a}^{2}}}\)
C√¢u 10: Hai ƒëi·ªán t√≠ch d∆∞∆°ng q ƒë·∫∑t t·∫°i A v√Ý B, \(AB=a\). X√°c ƒë·ªãnh v√©ct∆° c∆∞·ªùng ƒë·ªô ƒëi·ªán tr∆∞·ªùng t·∫°i ƒëi·ªÉm M tr√™n ƒë∆∞·ªùng trung tr·ª±c c·ªßa ƒëo·∫°n th·∫≥ng AB c√°ch trung ƒëi·ªÉm O c·ªßa AB m·ªôt ƒëo·∫°n \(OM=a\sqrt{3}/6\):
A. \(E=k\frac{q}{{{a}^{2}}}\), hướng theo trung trực của AB đi xa AB
B. \(E=k\frac{2q}{{{a}^{2}}}\), h∆∞·ªõng theo trung tr·ª±c c·ªßa AB ƒëi v√Ýo AB
C. \(E=k\frac{3q}{{{a}^{2}}}\), hướng theo trung trực của AB đi xa AB
D. \(E=k\frac{3q}{{{a}^{2}}}\), h∆∞·ªõng song song v·ªõi AB
ĐÁP ÁN
|
1-C |
2-D |
3-D |
4-A |
5-A |
6-C |
7-A |
8-C |
9-D |
10-C |
4. HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Đáp án C.
+ V√¨ \({{q}_{1}}\) v√Ý \({{q}_{2}}\) tr√°i d·∫•u nhau v√Ý M n·∫±m trong ƒë∆∞·ªùng th·∫≥ng n√™n ƒë·ªô l·ªõn c∆∞·ªùng ƒë·ªô ƒëi·ªán tr∆∞·ªùng t·∫°i ƒëi·ªÉm M l√Ý
\({{E}_{M}}={{E}_{1}}+{{E}_{2}}=\frac{k\left( \left| {{q}_{1}} \right|+\left| {{q}_{2}} \right| \right)}{{{r}^{2}}}=\frac{{{9.10}^{9}}{{.10.10}^{-9}}}{0,{{05}^{2}}}=36000\left( \text{V/m} \right)\)
Câu 2: Đáp án D.
+ T·ª´ gi·∫£ thi·∫øt suy ra ƒëi·ªÉm M n·∫±m ngo√Ýi ƒë∆∞·ªùng th·∫≥ng, l·∫°i c√≥ \({{q}_{1}}\) v√Ý \({{q}_{2}}\) tr√°i d·∫•u nhau n√™n ƒë·ªô l·ªõn c∆∞·ªùng ƒë·ªô ƒëi·ªán tr∆∞·ªùng t·∫°i ƒëi·ªÉm M l√Ý
\({{E}_{M}}=\left| {{E}_{1}}-{{E}_{2}} \right|=k\left| \frac{\left| {{q}_{1}} \right|}{r_{1}^{2}}+\frac{\left| {{q}_{2}} \right|}{r_{2}^{2}} \right|\)
\(={{9.10}^{9}}.\left| \frac{{{5.10}^{-9}}}{0,05_{{}}^{2}}-\frac{{{5.10}^{-9}}}{0,15_{{}}^{2}} \right|=16000\left( \text{V/m} \right)\)
Câu 3: Đáp án D.
+ G·ªçi M l√Ý trung ƒëi·ªÉm c·∫°nh BC, c∆∞·ªùng ƒë·ªô ƒëi·ªán tr∆∞·ªùng t·∫°i M
\(\overrightarrow{{{E}_{M}}}=\overrightarrow{{{E}_{A}}}+\overrightarrow{{{E}_{B}}}+\overrightarrow{{{E}_{C}}}\)
+ Vì \({{q}_{B}}={{q}_{C}}>0\) nên \(\overrightarrow{{{E}_{B}}}+\overrightarrow{{{E}_{C}}}=\vec{0}\Rightarrow \overrightarrow{{{E}_{M}}}=\overrightarrow{{{E}_{A}}}\)
+ \({{E}_{A}}=k.\frac{\left| q \right|}{A{{M}^{2}}}=\frac{{{9.10}^{9}}{{.10.10}^{-9}}}{0,{{1}^{2}}-0,{{05}^{2}}}=12000\left( \text{V/m} \right)\)
Câu 4: Đáp án A.
+ G·ªçi O l√Ý t√¢m c·ªßa t√¢m c·ªßa tam gi√°c ƒë·ªÅu, c∆∞·ªùng ƒë·ªô ƒëi·ªán tr∆∞·ªùng t·∫°i ƒëi·ªÉm O
\(\overrightarrow{{{E}_{O}}}=\overrightarrow{{{E}_{A}}}+\overrightarrow{{{E}_{B}}}+\overrightarrow{{{E}_{C}}}=\overrightarrow{{{E}_{B}}}+\overrightarrow{{{E}_{AC}}}\), khi t·ªïng h·ª£p vect∆° ta ƒë∆∞·ª£c \(\overrightarrow{{{E}_{B}}},\overrightarrow{{{E}_{AC}}}\) l√Ý 2 vect∆° c√≥ c√πng ph∆∞∆°ng nh∆∞ng ng∆∞·ª£c chi·ªÅu \(\Rightarrow {{E}_{O}}=\left| {{E}_{B}}-{{E}_{AC}} \right|\)
+ V√¨ \(OA=OB=OC\) v√Ý \({{q}_{A}}={{q}_{B}}={{q}_{C}}\) n√™n \({{E}_{A}}={{E}_{B}}={{E}_{C}}=\frac{k\left| q \right|}{O{{A}^{2}}}=\frac{{{9.10}^{9}}{{.10.10}^{-9}}}{\frac{4}{9}\left( 0,{{1}^{2}}-0,{{05}^{2}} \right)}=27000\left( \text{V/m} \right)\)
+ \({{E}_{A}}={{E}_{C}},\left( \overrightarrow{{{E}_{A}}},\overrightarrow{{{E}_{C}}} \right)={{120}^{0}}\Rightarrow {{E}_{A}}={{E}_{C}}={{E}_{AC}}\)
\(\Rightarrow {{E}_{O}}=\left| {{E}_{B}}-{{E}_{AC}} \right|=0\,\,\text{V/m}\)
Câu 5: Đáp án A.
+ G·ªçi \(\alpha \) l√Ý g√≥c h·ª£p b·ªüi vect∆° l·ª±c \(\overrightarrow{F}\) v√Ý tr·ª•c Oy, ta c√≥: \(\tan \alpha =\frac{{{E}_{X}}}{{{E}_{Y}}}=-\frac{1}{\sqrt{3}}\Rightarrow \alpha ={{150}^{0}}\)
+ \(F=\left| q \right|E=\left| q \right|.\frac{\left| {{E}_{Y}} \right|}{\cos \left( {{30}^{0}} \right)}=0,03\,\,\text{N}\)
Câu 6: Đáp án C.
+ Ta xác định cường độ điện trường đặt tại điểm A của tam giác ABC
\(\overrightarrow{{{E}_{A}}}=\overrightarrow{{{E}_{B}}}+\overrightarrow{{{E}_{C}}}\), v√¨ tam gi√°c ABC l√Ý tam gi√°c ƒë·ªÅu, \({{q}_{A}}={{q}_{B}}={{q}_{C}},\left( \overrightarrow{{{E}_{B}}},\overrightarrow{{{E}_{C}}} \right)={{60}^{0}}\)
\(\Rightarrow {{E}_{BC}}=2{{E}_{B}}\cos {{30}^{0}}=2.\frac{k\left| q \right|}{{{a}^{2}}}.\frac{\sqrt{3}}{2}=\frac{k\left| q \right|\sqrt{3}}{{{a}^{2}}}={{E}_{A}}\)
Câu 7: Đáp án A.
Tưong tự câu 6 nhưng chú ý ở đây vì 2 điện tích trái dấu nên \(\left( \overrightarrow{{{E}_{B}}},\overrightarrow{{{E}_{C}}} \right)={{120}^{0}}\Rightarrow {{E}_{BC}}={{E}_{a}}={{E}_{B}}=\frac{k\left| q \right|}{{{a}^{2}}}\)
Câu 8: Đáp án C.
+ Vì bốn điện tích điểm cùng dấu cùng độ lớn nên tại tâm của hình vuông cường độ điện trường gây ra bởi bốn điện tích đó bằng 0
Câu 9: Đáp án D.
+ G·ªçi t√¢m c·ªßa h√¨nh vu√¥ng l√Ý O, c∆∞·ªùng ƒë·ªô ƒëi·ªán tr∆∞·ªùng t·∫°i O l√Ý: \(\overrightarrow{{{E}_{O}}}=\overrightarrow{{{E}_{A}}}+\overrightarrow{{{E}_{B}}}+\overrightarrow{{{E}_{C}}}+\overrightarrow{{{E}_{D}}}\)
+ V√¨ c√°c ƒëi·ªán t√≠ch c√πng d·∫•u k·ªÅ nhau v√Ý c√≥ 2 ƒëi·ªán t√≠ch √¢m 2 ƒëi·ªán t√≠ch d∆∞∆°ng v√Ý AC vu√¥ng g√≥c v·ªõi BD
\({{E}_{O}}=\sqrt{{{\left( {{E}_{A}}+{{E}_{C}} \right)}^{2}}+{{\left( {{E}_{B}}+{{E}_{D}} \right)}^{2}}}\), vì 4 điện tích có cùng độ lớn q, \(OA=OB=OC=OD\)
\(\Rightarrow {{E}_{A}}={{E}_{B}}={{E}_{C}}={{E}_{D}}=\frac{k\left| q \right|}{{{\left( \frac{a}{\sqrt{2}} \right)}^{2}}}=\frac{2k\left| q \right|}{{{a}^{2}}}\)
+ \({{E}_{O}}=\sqrt{8E_{A}^{2}}=\frac{4k\left| q \right|\sqrt{2}}{{{a}^{2}}}\)
Câu 10: Đáp án C.
+ Cường độ điện trường tại điểm M:
\(\overrightarrow{{{E}_{M}}}=\overrightarrow{{{E}_{A}}}+\overrightarrow{{{E}_{B}}}\)
+ Đặt \(\widehat{AMB}=\alpha \), ta có:
\(\cos \frac{\alpha }{2}=\frac{OM}{MA}=\frac{OM}{\sqrt{O{{M}^{2}}+O{{A}^{2}}}}=\frac{a\frac{\sqrt{3}}{6}}{\sqrt{\frac{{{a}^{2}}}{12}+\frac{{{a}^{2}}}{4}}}=\frac{1}{2}\)
+ Ta có \({{E}_{A}}={{E}_{B}},\left( \overrightarrow{{{E}_{A}}},\overrightarrow{{{E}_{B}}} \right)=\alpha \)
\(\Rightarrow {{E}_{M}}=2{{E}_{A}}\cos \left( \frac{\alpha }{2} \right)={{E}_{A}}=\frac{k\left| q \right|}{M{{A}^{2}}}=\frac{k3\left| q \right|}{{{a}^{2}}}\)
Vectơ cường độ điện trường tại M có hướng theo trung trực của AB đi xa AB.
---(H·∫øt )---
Tr√™n ƒë√¢y l√Ý to√Ýn b·ªô n·ªôi dung t√Ýi li·ªáu Chuy√™n ƒë·ªÅ S·ª± ch·ªìng ch·∫•t ƒëi·ªán tr∆∞·ªùng - ƒêi·ªán tr∆∞·ªùng t·ªïng h·ª£p m√¥n V·∫≠t L√Ω 11 nƒÉm 2021. ƒê·ªÉ xem th√™m nhi·ªÅu t∆∞ li·ªáu h·ªØu √≠ch kh√°c, c√°c em ƒëƒÉng nh·∫≠p v√Ýo trang hoc247.net ƒë·ªÉ t·∫£i t√Ýi li·ªáu v·ªÅ m√°y t√≠nh.
Hy v·ªçng t√Ýi li·ªáu n√Ýy s·∫Ω gi√∫p c√°c em h·ªçc sinh √¥n t·∫≠p t·ªët v√Ý ƒë·∫°t th√Ýnh t√≠ch cao trong h·ªçc t·∫≠p.
Tư liệu nổi bật tuần
- Xem thêm


