-
Câu hỏi:
Tìm tập hợp các giá trị của tham số thực m để hàm số \(y = \sqrt {{x^2} + 1} - mx - 1\) đồng biến trên khoảng \(\left( { - \infty ; + \infty } \right).\)
-
A.
\(\left( { - \infty ;1} \right)\)
-
B.
\(\left[ {1; + \infty } \right)\)
-
C.
\(\left[ { - 1;1} \right]\)
-
D.
\(\left( { - \infty ; - 1} \right]\)
Lời giải tham khảo:
Đáp án đúng: D
Hàm số \(y = \sqrt {{x^2} + 1} - mx - 1\)
\(y' = \frac{x}{{\sqrt {{x^2} + 1} }} - m\)
Hàm số luôn đồng biến khi và chi khi \(m \le \frac{x}{{\sqrt {{x^2} + 1} }}.\)
Xét hàm số \(f(x) = \frac{x}{{\sqrt {{x^2} + 1} }}\)
\(f'(x) = \frac{1}{{\sqrt {{{({x^2} + 1)}^3}} }} > 0,\forall x\)
Suy ra f(x) luôn đồng biến trên \(\mathbb{R}\)
Mặt khác \(\mathop {\lim }\limits_{x \to - \infty } \frac{x}{{\sqrt {{x^2} + 1} }} = - 1\)
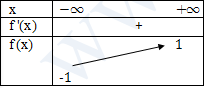
Vậy để hàm số đồng biến trên \(\mathbb{R}\) thì \(m \le - 1.\)
Hãy trả lời câu hỏi trước khi xem đáp án và lời giải -
A.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
CÂU HỎI KHÁC
- Cho hàm số \(y = {x^2}(3 - x).\) Mệnh đề nào sau đây là đúng?
- Cho hàm số \(y = \sqrt {{x^2} - 1} .\) Mệnh đề nào dưới đây đúng?
- Tìm tất cả các giá trị thực của m để hàm số \(y = {x^3} - m{x^2} + 3x + 4\) đồng biến trên \(\mathbb{R}\)
- Tìm tập hợp các giá trị của tham số thực m để hàm số \(y = \sqrt {{x^2} + 1} - mx - 1\) đồng biến trên khoảng \(\left( { - \infty ; + \infty } \right).\)
- Tìm tập hợp tất cả giá trị thực của tham số m sao cho hàm số \(y = \frac{{\left( {m + 1} \right)x + 2m + 2}}{{x + m}}\) nghịch biến trên khoảng \(\left( { - 1; + \infty } \right)\).
- Tập xác định của hàm số \(f\left( x \right) = - {x^3} + 3{{{x}}^2} - 2\) là:
- Cho hàm số \(y = {x^3} - 2{{m{x}}^2} + x + 1\). Mệnh đề nào sau đây là đúng?
- Hàm số \(y = 2{{m{x}}^3} + 3{{m{x}}^2} + 1\) nghịch biến trên khoảng (hoặc các khoảng) nào sau đây:
- Cho hàm số \(\frac{1}{3}{x^3} - \frac{1}{2}{x^2} - 12{m{x}} - 1\). Mệnh đề nào đúng?
- Hàm số \(y = \frac{{{x^3}}}{3} - {x^2} + x\) đồng biến trên khoảng nào?

